Question

In an isosceles triangle ABC, the vertex A is \((6, 1)\) and the equation of the base BC is \(2x + y = 4\). Let the point B lie on the line \(x + 3y = 7\). If \((α, β)\) is the centroid of ΔABC, then \(15(α + β)\) is equal to :

• A. 39
• B. 41
• C. 51
• D. 63

Answer 1

The Correct Option is C

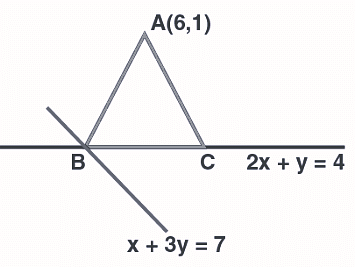
\(2x+y = 4\)  …….. (1)
\(2x+6y = 14\)   …….. (2)
On solving eq(1) and eq(2)
\(y = 2, \ x = 3\)
\(B(1, 2)\) and \(C(k, 4 – 2k)\)
Hence, \(AB^2 = AC^2\)
\(52 + (–1)^2 = (6 – k)^2 + (–3 + 2k)^2\)
\(⇒ 5k^2 – 24k + 19 = 0\)
\((5k – 19)(k – 1) = 0\)
\(⇒ k=\)\(\frac {19}{5}\)

\(C\) \((\frac {19}{5}\),−\(\frac {18}{5})\) ⇒ Centroid \((α, β)\)

\(α = \frac {6+1+\frac {19}{5}}{3}\)
\(α = \frac {18}{5}\)
\(β = \frac {1+2-\frac {18}{5}}{3}\)

\(β= -\frac 15\)

Now \(15(α + β)\) \(= 15(\frac {18}{5}+(-\frac 15))\)
\(=15 \times \frac {17}{5}\)
\(= 51\)

So, the answer is (C): \(51\).