Question:
In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
Updated On: Mar 15, 2025
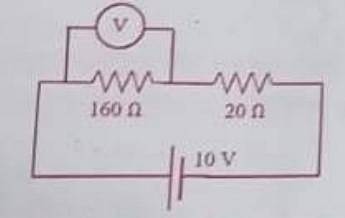
- 20Ω
- 320Ω
- 160Ω
- 1.44kΩ
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Given the values: I=10Ω8 volts=5/4=0.8 AI=8 volts10Ω=45=0.8 A Voltage across 5Ω5Ω: V1=(0.8)×5=V1=4 volts
Hence, the electromotive force (e.m.f) of the battery is equal to the voltage across 10Ω10Ω, which is:
EMF=8+4=EMF=12 voltsEMF=8+4=EMF=12 volts
Therefore, the correct option is 160Ω.
The correct option is(C): 160Ω
Was this answer helpful?
4
25
Top Questions on Resistance
A battery of \( 6 \, \text{V} \) is connected to the circuit as shown below. The current \( I \) drawn from the battery is:
- MHT CET - 2024
- Physics
- Resistance
- Resistance of a wire is \( 8\Omega \). It is drawn in such a way that it experiences a longitudinal strain of \( 400% \). The final resistance of the wire is:
- AP EAMCET - 2024
- Physics
- Resistance
- A resistor of resistance \( R \), inductor of inductive reactance \( 2R \) and a capacitor of capacitive reactance \( X_C \) are connected in series to an A.C. source. If the series LCR circuit is in resonance, then the power factor of the circuit and the value \( X_C \) are respectively:
- AP EAMCET - 2024
- Physics
- Resistance
- A cell of emf 1.2 V and internal resistance 2 \( \Omega \) is connected in parallel to another cell of emf 1.5 V and internal resistance 1 \( \Omega \). If the like poles of the cells are connected together, the emf of the combination of the two cells is:
- AP EAMCET - 2024
- Physics
- Resistance
- Two wires A and B are made up of the same material and have the same mass. Wire A has radius \(2.0 \, \text{mm}\) and wire B has radius \(4.0 \, \text{mm}\). The resistance of wire B is \(2 \, \Omega\). The resistance of wire A is _____ \( \Omega \).
- JEE Main - 2024
- Physics
- Resistance
View More Questions
Questions Asked in WBJEE exam
- Two straight conducting plates form an angle θ where their ends are joined. A conducting bar in contact with the plates and forming an isosceles triangle with them, starts at the vertex at time t = 0 and moves with constant velocity v to the right as shown in the figure. A magnetic field B points out of the page. The magnitude of emf induced at t = 1 second will be:
- WBJEE - 2024
- Electromagnetic induction
- A 2V cell is connected across the points A and B as shown in the figure. Assume that the resistance of each diode is zero in forward bias and infinity in reverse bias. The current supplied by the cell is:
- WBJEE - 2024
- Current electricity
- Consider a circuit where a cell of emf \( E_0 \) and internal resistance \( r \) is connected across the terminal A and B as shown in the figure. The value of \( R \) for which the power generated in the circuit is maximum, is given by:
- WBJEE - 2024
- Current electricity
- In a series LCR circuit, the rms voltage across the resistor and the capacitor are \(30 \, \text{V}\) and \(90 \, \text{V}\) respectively. If the applied voltage is \(50\sqrt{2}\sin\omega t\), then the peak voltage across the inductor is:
- WBJEE - 2024
- Alternating current
- Which of the following statement(s) is/are true in respect of nuclear binding energy?
(i) The mass energy of a nucleus is larger than the total mass energy of its individual protons and neutrons.
(ii) If a nucleus could be separated into its nucleons, an energy equal to the binding energy would have to be transferred to the particles during the separating process.
(iii) The binding energy is a measure of how well the nucleons in a nucleus are held together.
(iv) The nuclear fission is somehow related to acquiring higher binding energy.- WBJEE - 2024
- Nuclear physics
View More Questions
Concepts Used:
Resistance
Resistance is the measure of opposition applied by any object to the flow of electric current. A resistor is an electronic constituent that is used in the circuit with the purpose of offering that specific amount of resistance.
R=V/I
In this case,
v = Voltage across its ends
I = Current flowing through it
All materials resist current flow to some degree. They fall into one of two broad categories:
- Conductors: Materials that offer very little resistance where electrons can move easily. Examples: silver, copper, gold and aluminum.
- Insulators: Materials that present high resistance and restrict the flow of electrons. Examples: Rubber, paper, glass, wood and plastic.
Resistance measurements are normally taken to indicate the condition of a component or a circuit.
- The higher the resistance, the lower the current flow. If abnormally high, one possible cause (among many) could be damaged conductors due to burning or corrosion. All conductors give off some degree of heat, so overheating is an issue often associated with resistance.
- The lower the resistance, the higher the current flow. Possible causes: insulators damaged by moisture or overheating.