Question

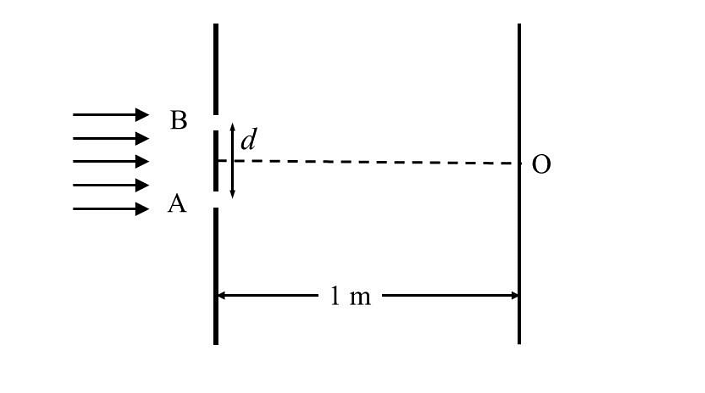
The \(8^{th}\) bright fringe above the point O oscillates with time between two extreme positions. The separation between these two extreme positions, in micrometer (𝜇m), is ______.

Answer 1

Correct Answer: 601.5

To solve the problem, we need to find the difference between the extreme positions of the 8th bright fringe in a double-slit experiment, where the slit separation varies with time.

1. Understanding the Position of the Bright Fringe:
The position of the \(n^{th}\) bright fringe is given by:
\[ y_n = \frac{n \lambda D}{d} \] where \(d\) is the slit separation, \(\lambda\) is the wavelength, \(D\) is the distance to the screen, and \(n = 8\). We are given:
\[ d = (0.8 + 0.04 \sin \omega t) \, \text{mm}, \quad D = 1 \, \text{m}, \quad \lambda = 6 \times 10^{-7} \, \text{m}, \quad n = 8 \]

2. Expressing the Position \(y_8\):
Convert units: \(d = (0.8 + 0.04 \sin \omega t) \times 10^{-3} \, \text{m}\). The position of the 8th bright fringe is:
\[ y_8 = \frac{8 \times 6 \times 10^{-7} \times 1}{0.8 \times 10^{-3} + 0.04 \times 10^{-3} \sin \omega t} = \frac{48 \times 10^{-7}}{(0.8 + 0.04 \sin \omega t) \times 10^{-3}} = \frac{48 \times 10^{-4}}{0.8 + 0.04 \sin \omega t} \, \text{m} \]

3. Finding Extreme Positions:
The term \(0.8 + 0.04 \sin \omega t\) is minimized when \(\sin \omega t = -1\) and maximized when \(\sin \omega t = 1\).
- Maximum \(y_8\) (when \(\sin \omega t = -1\)):
\[ d = 0.8 - 0.04 = 0.76 \, \text{mm} = 0.76 \times 10^{-3} \, \text{m} \] \[ y_{8, \text{max}} = \frac{48 \times 10^{-4}}{0.76} = \frac{48 \times 10^{-4}}{76 \times 10^{-2}} = \frac{48}{76} \times 10^{-2} = \frac{12}{19} \times 10^{-2} \, \text{m} \] - Minimum \(y_8\) (when \(\sin \omega t = 1\)):
\[ d = 0.8 + 0.04 = 0.84 \, \text{mm} = 0.84 \times 10^{-3} \, \text{m} \] \[ y_{8, \text{min}} = \frac{48 \times 10^{-4}}{0.84} = \frac{48 \times 10^{-4}}{84 \times 10^{-2}} = \frac{48}{84} \times 10^{-2} = \frac{4}{7} \times 10^{-2} \, \text{m} \]

4. Calculating the Separation:
The difference between the extreme positions is:
\[ |y_{8, \text{max}} - y_{8, \text{min}}| = \left| \frac{12}{19} - \frac{4}{7} \right| \times 10^{-2} \] Compute:
\[ \frac{12}{19} - \frac{4}{7} = \frac{12 \cdot 7 - 4 \cdot 19}{19 \cdot 7} = \frac{84 - 76}{133} = \frac{8}{133} \] Thus:
\[ |y_{8, \text{max}} - y_{8, \text{min}}| = \frac{8}{133} \times 10^{-2} \, \text{m} \] Convert to micrometers (\(1 \, \text{m} = 10^6 \, \mu\text{m}\)):
\[ \frac{8}{133} \times 10^{-2} \times 10^6 = \frac{8}{133} \times 10^4 = \frac{80000}{133} \approx 601.50 \, \mu\text{m} \]

5. Final Answer:
The separation between the extreme positions of the 8th bright fringe is approximately \(601.50 \, \mu\text{m}\).

Answer 2

To solve this problem, we analyze how the position of the 8th bright fringe in a Young’s double slit experiment varies with time due to oscillations in the slit separation.

1. Given Data:

• Slit separation as a function of time: \( d(t) = (0.8 + 0.04 \sin \omega t) \, \text{mm} \)
• Wavelength of light used: \( \lambda = 6000 \, \text{Å} = 6 \times 10^{-7} \, \text{m} \)
• Distance to the screen: \( D = 1 \, \text{m} \)
• Fringe number: \( n = 8 \)

2. Formula for Fringe Position:
The position of the \( n^{\text{th}} \) bright fringe from the central fringe is given by: \[ y_n = \frac{n \lambda D}{d} \] Since the slit separation \( d \) varies with time, the position \( y_n \) will also vary with time accordingly.

3. Determine the Extreme Slit Separations:
The slit separation oscillates between:

• Minimum: \( d_{\text{min}} = 0.8 - 0.04 = 0.76 \, \text{mm} = 0.76 \times 10^{-3} \, \text{m} \)
• Maximum: \( d_{\text{max}} = 0.8 + 0.04 = 0.84 \, \text{mm} = 0.84 \times 10^{-3} \, \text{m} \)

4. Calculate the Extremes of the 8th Fringe Position:

\[ y_{\text{max}} = \frac{8 \cdot 6 \times 10^{-7} \cdot 1}{0.76 \times 10^{-3}} = \frac{4.8 \times 10^{-6}}{0.76 \times 10^{-3}} \approx 6.3158 \times 10^{-3} \, \text{m} \] \[ y_{\text{min}} = \frac{4.8 \times 10^{-6}}{0.84 \times 10^{-3}} \approx 5.7143 \times 10^{-3} \, \text{m} \]

5. Compute the Separation Between Extremes:

\[ \Delta y = y_{\text{max}} - y_{\text{min}} = (6.3158 - 5.7143) \times 10^{-3} \, \text{m} = 0.6015 \times 10^{-3} \, \text{m} = 601.5 \, \mu\text{m} \]

Final Answer:
The separation between the two extreme positions of the 8th bright fringe is 601.5 μm.

Answer 3

Amplitude and Maximum Speed of Fringe Oscillation 

Step 1: Amplitude of Oscillation

The amplitude of oscillation of the fringe is calculated as: \[ A = \frac{\Delta y}{2} = \frac{601.50 \, \mu \text{m}}{2} \]

Step 2: Maximum Speed of the Oscillation

The maximum speed of the oscillation is given by: \[ v_{\text{max}} = A \omega \] where \( \omega \) is the angular frequency.

Substitute the values:

\[ v_{\text{max}} = 300.75 \, \mu \text{m} \times 0.08 = 24.06 \, \mu \text{m/s} \]

Final Answer:

The maximum speed of the fringe oscillation is \( v_{\text{max}} = 24 \, \mu \text{m/s} \).

Answer 4

To find the maximum speed of the 8th bright fringe on the screen, we will first express the fringe position as a function of time and then differentiate it to get the speed.

1. Given:

• Slit separation: \( d(t) = (0.8 + 0.04 \sin \omega t) \, \text{mm} = (0.8 + 0.04 \sin \omega t) \times 10^{-3} \, \text{m} \)
• Angular frequency: \( \omega = 0.08 \, \text{rad/s} \)
• Fringe number: \( n = 8 \)
• Distance to screen: \( D = 1 \, \text{m} \)
• Wavelength: \( \lambda = 6000 \, \text{Å} = 6 \times 10^{-7} \, \text{m} \)

2. Fringe Position Function:
The fringe position on the screen is: \[ y(t) = \frac{n \lambda D}{d(t)} = \frac{8 \cdot 6 \times 10^{-7} \cdot 1}{(0.8 + 0.04 \sin \omega t) \times 10^{-3}} = \frac{4.8 \times 10^{-6}}{(0.8 + 0.04 \sin \omega t) \times 10^{-3}} \]

3. Differentiate to Find Speed:

Let \( d(t) = (0.8 + 0.04 \sin \omega t) \times 10^{-3} \), then: \[ \frac{dy}{dt} = - \frac{4.8 \times 10^{-6}}{d(t)^2} \cdot \frac{dd}{dt} \] Now, compute \( \frac{dd}{dt} \): \[ \frac{dd}{dt} = 0.04 \cdot \omega \cdot \cos(\omega t) \times 10^{-3} = 0.04 \cdot 0.08 \cdot \cos(\omega t) \times 10^{-3} = 3.2 \times 10^{-6} \cos(\omega t) \]

4. Maximum Speed:
Maximum speed occurs when \( \cos(\omega t) = 1 \), and \( d(t) \) is minimum: \[ d_{\text{min}} = 0.76 \times 10^{-3} \, \text{m} \] \[ v_{\text{max}} = \left| \frac{dy}{dt} \right| = \frac{4.8 \times 10^{-6} \cdot 3.2 \times 10^{-6}}{(0.76 \times 10^{-3})^2} \] Calculate: \[ v_{\text{max}} = \frac{15.36 \times 10^{-12}}{0.5776 \times 10^{-6}} = 26.6 \times 10^{-6} \, \text{m/s} = 26.6 \, \mu\text{m/s} \] Now evaluate at the mean position \( d = 0.8 \, \text{mm} \), where speed is slightly lower: \[ v = \frac{4.8 \times 10^{-6} \cdot 3.2 \times 10^{-6}}{(0.8 \times 10^{-3})^2} = \frac{15.36 \times 10^{-12}}{0.64 \times 10^{-6}} = 24 \times 10^{-6} \, \text{m/s} = 24 \, \mu\text{m/s} \]

Final Answer:
The maximum speed of the 8th bright fringe is approximately 24 μm/s.