Question:
If the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are $a, b$ and $c$ respectively, the ratio between' the increase in lengths of brass and steel wires would be
If the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are $a, b$ and $c$ respectively, the ratio between' the increase in lengths of brass and steel wires would be
Updated On: Dec 17, 2025
- $\frac{b^2 a}{2c}$
- $\frac{bc}{2a^2}$
- $\frac{ba^2 }{2c}$
- $\frac{2b^2c}{a}$
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Free body diagram of the two blocks are
Given, $\frac{l_{1}}{l_{2} } = a, \frac{r_{1}}{r_{2}} = b , \frac{Y_{1}}{Y_{2}} $
Let Young's modulus of steel is $Y_1$ and of brass is $Y_2$
$ \therefore \, \, Y_{1} = \frac{F_{1}. l_{1}}{A_{1} . \Delta l_{1}}$ ......(i)
And $ Y_{2} = \frac{F_{2}.l_{2}}{A_{2} \Delta l_{2}} $ ....(ii)
Diving E (i) by E (ii), we get
$\frac{Y_{1}}{Y_{2} } = \frac{\frac{F_{1}l_{1}}{A_{1}l_{1}}}{\frac{F_{2}.l_{2}}{A_{2} . \Delta l_{2}}} $
Or $\frac{Y_{1}}{Y_{2} } = \frac{F_{1}.A_{2} .l_{1}. \Delta l_{2}}{F_{2} .A_{1} .l_{2} . \Delta l_{1}} $ ........(iii)
Force on steel wire from free body diagram
$T= F_{1} = \left(2g\right) $ newton
Force on brass wire from free body diagram
$F_{2} = T� = T + 2g = \left(4g\right) $newton
Now, putting the value of $F_1, F_2$, in E (iii), we get
$\frac{Y_{1}}{Y_{2} } = \frac{2g}{4g} . \frac{\pi r^{2}_{2}}{\pi r^{2}_{1}} . \frac{l_{2}}{l_{2}} . \frac{\Delta l_{2}}{\Delta l_{1}} $
Or $c = \frac{1}{2} \frac{1}{b^{2} } . a \frac{\Delta l_{2}}{\Delta l_{1}} $
Or $ \frac{\Delta l_{1}}{\Delta l_{2}} = \frac{a}{2b^{2} c }$
Given, $\frac{l_{1}}{l_{2} } = a, \frac{r_{1}}{r_{2}} = b , \frac{Y_{1}}{Y_{2}} $
Let Young's modulus of steel is $Y_1$ and of brass is $Y_2$
$ \therefore \, \, Y_{1} = \frac{F_{1}. l_{1}}{A_{1} . \Delta l_{1}}$ ......(i)
And $ Y_{2} = \frac{F_{2}.l_{2}}{A_{2} \Delta l_{2}} $ ....(ii)
Diving E (i) by E (ii), we get
$\frac{Y_{1}}{Y_{2} } = \frac{\frac{F_{1}l_{1}}{A_{1}l_{1}}}{\frac{F_{2}.l_{2}}{A_{2} . \Delta l_{2}}} $
Or $\frac{Y_{1}}{Y_{2} } = \frac{F_{1}.A_{2} .l_{1}. \Delta l_{2}}{F_{2} .A_{1} .l_{2} . \Delta l_{1}} $ ........(iii)
Force on steel wire from free body diagram
$T= F_{1} = \left(2g\right) $ newton
Force on brass wire from free body diagram
$F_{2} = T� = T + 2g = \left(4g\right) $newton
Now, putting the value of $F_1, F_2$, in E (iii), we get
$\frac{Y_{1}}{Y_{2} } = \frac{2g}{4g} . \frac{\pi r^{2}_{2}}{\pi r^{2}_{1}} . \frac{l_{2}}{l_{2}} . \frac{\Delta l_{2}}{\Delta l_{1}} $
Or $c = \frac{1}{2} \frac{1}{b^{2} } . a \frac{\Delta l_{2}}{\Delta l_{1}} $
Or $ \frac{\Delta l_{1}}{\Delta l_{2}} = \frac{a}{2b^{2} c }$
Was this answer helpful?
0
0
Top Questions on elastic moduli
- The slope of the stress-strain curve in the elastic deformation region is
- JKCET - 2024
- Physics
- elastic moduli
- The law which states that within elastic limits strain produced is proportional to the stress producing it is known as
- JKCET - 2024
- Physics
- elastic moduli
- A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5 cm. Another wire of the same material of length 4L and radius 4r is pulled by a force 4F under same conditions. The increase in length of this wire is ___ cm.
- JEE Main - 2022
- Physics
- elastic moduli
The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
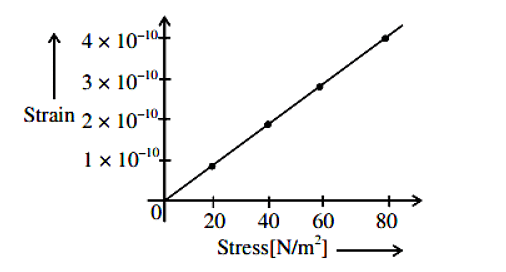
- JEE Main - 2022
- Physics
- elastic moduli
- If the length of a wire is made double and radius is halved of its respective values. Then, the Young’s modulus of the material of the wire will :
- JEE Main - 2022
- Physics
- elastic moduli
View More Questions
Questions Asked in BITSAT exam
- What is the dot product of the vectors \( \mathbf{a} = (2, 3, 1) \) and \( \mathbf{b} = (1, -1, 4) \)?
- BITSAT - 2025
- Vector Algebra
- Find the determinant of the matrix \( A = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} \).
- BITSAT - 2025
- Matrices
- A convex lens has focal length 20 cm. An object is placed at a distance of 40 cm from the lens. What is the position of the image formed?
- BITSAT - 2025
- Ray optics and optical instruments
- What is the value of \( \sin 30^\circ \)?
- BITSAT - 2025
- Trigonometry
- The area enclosed between the curve \(y = \log_e(x + e)\) and the coordinate axes is:
- BITSAT - 2025
- Fundamental Theorem of Calculus
View More Questions