Question:
If \( A \) is the set of even natural numbers less than 8 and \( B \) is the set of prime numbers less than 7, then the number of relations from \( A \) to \( B \) is:
If \( A \) is the set of even natural numbers less than 8 and \( B \) is the set of prime numbers less than 7, then the number of relations from \( A \) to \( B \) is:
Show Hint
The number of relations between two sets \( A \) and \( B \) is \( 2^{|A \times B|} \), where \( |A \times B| \) is the number of ordered pairs in the Cartesian product of \( A \) and \( B \).
Updated On: Dec 11, 2025
- \( 2^9 \)
- \( 9 \)
- \( 3^2 \)
- \( 2^9 - 1 \)
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
We are given two sets:
- \( A \) is the set of even natural numbers less than 8. Therefore, \( A = \{2, 4, 6\} \).
- \( B \) is the set of prime numbers less than 7. Therefore, \( B = \{2, 3, 5\} \).
A relation from set \( A \) to set \( B \) is any subset of the Cartesian product \( A \times B \), which consists of all possible ordered pairs of elements from \( A \) and \( B \). The number of elements in \( A \times B \) is the product of the number of elements in \( A \) and \( B \):
\[
|A \times B| = |A| \times |B| = 3 \times 3 = 9
\]
The number of relations from \( A \) to \( B \) is the number of subsets of \( A \times B \), which is \( 2^{|A \times B|} \). Since \( |A \times B| = 9 \), the number of relations is:
\[
2^9
\]
Thus, the correct answer is \( \boxed{2^9} \).
Was this answer helpful?
0
0
Top Questions on Sets
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
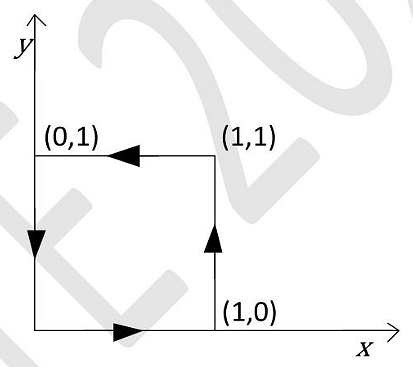
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
View More Questions
Questions Asked in IPU CET exam
- The pair of equations \( x + 3y = 6 \) and \( 2x - 3y = 12 \) :
- IPU CET - 2023
- System of Linear Equations
- If y intercept of a plane \( (x - y + z - 1) + q(x + y - z - 1) = 0 \) is 3 then q is :
- IPU CET - 2023
- 3-dimensional coordinate geometry
- If a, b, c are nonzero vectors such that a=8b, and c= -7b, then the angle between a and c is:
- IPU CET - 2023
- Vector Algebra
- If \( \sin y = x \sin(a + y) \), then \( \frac{dy}{dx} \) is:
- IPU CET - 2023
- Derivatives
- The value of \( x \), if \( \left| 5^2 - 4 \right| = 12x - 4 \), is:
- IPU CET - 2023
- Algebra
View More Questions