Given the following sets:
𝐴 = {2, 4, 6, 8, 10, 12}
𝐵 = {8, 10, 12, 14, 16, 18}
𝐶 = {7, 8, 9, 10 11, 12, 13}
(𝐴 ∩ 𝐵) ∪ (𝐵 ∩ 𝐶) is
𝐴 = {2, 4, 6, 8, 10, 12}
𝐵 = {8, 10, 12, 14, 16, 18}
𝐶 = {7, 8, 9, 10 11, 12, 13}
(𝐴 ∩ 𝐵) ∪ (𝐵 ∩ 𝐶) is
- {8, 10, 12, 14}
- {8, 10, 12}
- {7, 8, 10, 11, 12, 13, 14}
- {4, 6, 7, 8 10, 11, 12, 13}
The Correct Option is B
Solution and Explanation
To solve this problem, we need to find the union of two sets: \( (A \cap B) \) and \( (B \cap C) \).
- Intersection of Set A and Set B:
Set \( A = \{2, 4, 6, 8, 10, 12\} \) and Set \( B = \{8, 10, 12, 14, 16, 18\} \).
The intersection \( A \cap B \) includes all elements common to both sets A and B.
\( A \cap B = \{8, 10, 12\} \).
- Intersection of Set B and Set C:
Set \( B = \{8, 10, 12, 14, 16, 18\} \) and Set \( C = \{7, 8, 9, 10, 11, 12, 13\} \).
The intersection \( B \cap C \) includes all elements common to both sets B and C.
\( B \cap C = \{8, 10, 12\} \).
- Union of Intersections:
The union of \( A \cap B \) and \( B \cap C \) combines all elements from both intersections, without repeating any elements.
\( (A \cap B) \cup (B \cap C) = \{8, 10, 12\} \cup \{8, 10, 12\} = \{8, 10, 12\} \).
Since both intersections are identical, the union remains the same set of elements.
Conclusion: The result of the operation \( (A \cap B) \cup (B \cap C) \) is the set \(\{8, 10, 12\}\). Therefore, the correct option is
{8, 10, 12}
.
Top Questions on Sets
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
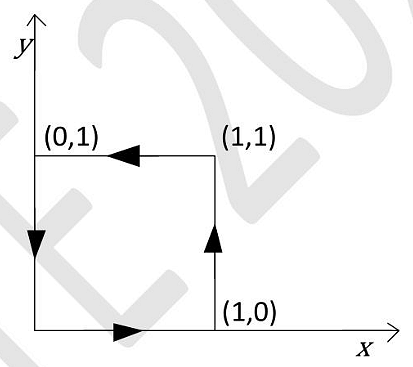
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
Questions Asked in IIT JAM BT exam
- The wavelength of a photon emitted during a transition from \( n = 3 \) to \( n = 2 \) state in the H atom is .............. nm. (answer in integer).
- IIT JAM BT - 2025
- Biotechnology
- The porphyrin ring (tetrapyrrole structure) is NOT found in functional
- IIT JAM BT - 2025
- Biotechnology
Identify the taxa that constitute a paraphyletic group in the given phylogenetic tree.

- IIT JAM BT - 2025
- Genetics
The vector, shown in the figure, has promoter and RBS sequences in the 300 bp region between the restriction sites for enzymes X and Y. There are no other sites for X and Y in the vector. The promoter is directed towards the Y site. The insert containing only an ORF provides 3 fragments after digestion with both enzymes X and Y. The ORF is cloned in the correct orientation in the vector using the single restriction enzyme Y. The size of the largest fragment of the recombinant plasmid expressing the ORF upon digestion with enzyme X is ........... bp. (answer in integer)

- IIT JAM BT - 2025
- Biotechnology
- Match the animals in Group I with the major form of excreted nitrogen metabolite in Group II. \[ \begin{array}{c|c} \text{Group I} & \text{Group II} \\ \hline P:\; \text{Bony fishes} & 3:\; \text{Ammonia} \\ Q:\; \text{Lions} & 1:\; \text{Urea} \\ R:\; \text{Birds} & 2:\; \text{Uric acid} \\ \end{array} \]
- IIT JAM BT - 2025
- Metabolism