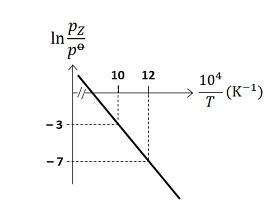
(Given, $\frac{ d (\ln K)}{ d \left(\frac{1}{T}\right)}=-\frac{\Delta H^{0}}{R}$, where the equilibrium constant, $K=\frac{p_{z}}{p^{0}}$ and the gas constant, $R=8314 \,J \,K ^{-1} mol ^{-1}$ )
The value of standard enthalpy, $\Delta H^{\phi}$ (in $kJ\, mol ^{-1}$ ) for the given reaction is ______
Correct Answer: 166.28
Solution and Explanation
The given reaction is: \[ X(s) \rightleftharpoons Y(s) + Z(g) \] The plot shows \( \ln \left( \frac{p_z}{p^\circ} \right) \) versus \( 10^4 / T \), where: - \( p_z \) is the pressure (in bar) of the gas Z at temperature \( T \), - \( p^\circ = 1 \, \text{bar} \), - The temperature range is \( 10^4 / T \), and the slope of the line from the plot is used to calculate the enthalpy change (\( \Delta H^\phi \)) for the reaction.
The formula provided is: \[ \frac{d (\ln K)}{d (1/T)} = -\frac{\Delta H^\phi}{R} \] where: - \( K = \frac{p_z}{p^\circ} \) is the equilibrium constant, - \( \Delta H^\phi \) is the standard enthalpy change of the reaction, - \( R = 8314 \, \text{J/molΒ·K} \) is the gas constant.
Step 2: Extracting the slope from the graph
From the graph, we can determine the change in \( \ln \left( \frac{p_z}{p^\circ} \right) \) and \( 10^4 / T \). The graph shows a line that has a slope between the points where \( 10^4 / T \) is 10 and 12.
- The change in \( \ln \left( \frac{p_z}{p^\circ} \right) \) is: \[ \Delta \left( \ln \left( \frac{p_z}{p^\circ} \right) \right) = -3 - (-7) = 4 \] - The change in \( 10^4 / T \) is: \[ \Delta \left( \frac{10^4}{T} \right) = 12 - 10 = 2 \] Thus, the slope of the line is: \[ m = \frac{4}{2} = 2 \] Step 3: Applying the slope to the formula
Now, we can use the relationship between the slope and \( \Delta H^\phi \): \[ \text{Slope} = -\frac{\Delta H^\phi}{R} \] Substituting the slope and the value of \( R \) (8314 J/molΒ·K): \[ 2 = -\frac{\Delta H^\phi}{8314} \] Solving for \( \Delta H^\phi \): \[ \Delta H^\phi = -2 \times 8314 = -16628 \, \text{J/mol} \] Step 4: Converting to kJ/mol
Converting the result to kJ/mol: \[ \Delta H^\phi = -16.628 \, \text{kJ/mol} \] Step 5: Conclusion
The value of the standard enthalpy change \( \Delta H^\phi \) for the given reaction is 166.28 kJ/mol.
The value of $\Delta S^{0}$ (in $J\, K ^{-1} mol ^{-1}$ ) for the given reaction, at $1000\, K$ is ______
Correct Answer: 141.34
Solution and Explanation
Step 1: Understanding the given data
The given reaction is:
\( X(s) \rightleftharpoons Y(s) + Z(g) \)
The plot shows \( \ln \left( \frac{p_z}{p^\circ} \right) \) versus \( \frac{10^4}{T} \), where:
- \( p_z \) is the pressure (in bar) of the gas Z at temperature \( T \),
- \( p^\circ = 1 \, \text{bar} \) (standard pressure),
- \( T \) is the temperature in Kelvin.
We are tasked with calculating the value of \( \Delta S^{0} \) at \( T = 1000 \, \text{K} \).
The relationship between the equilibrium constant \( K \) and temperature is given by:
\[ \frac{d (\ln K)}{d \left( \frac{1}{T} \right)} = -\frac{\Delta H^{0}}{R} \] - \( K = \frac{p_z}{p^\circ} \) is the equilibrium constant,
- \( \Delta H^{0} \) is the standard enthalpy change of the reaction,
Additionally, the equation for \( \Delta G^{0} \) (standard Gibbs free energy change) is:
\[ \Delta G^{0} = -RT \ln K \] And since \( \Delta G^{0} = \Delta H^{0} - T \Delta S^{0} \), we can relate \( \Delta S^{0} \) to the change in \( \Delta G^{0} \).
Step 2: Extracting information from the graph
From the graph, we can determine the slope. The change in \( \ln \left( \frac{p_z}{p^\circ} \right) \) is:
\[ \Delta \left( \ln \left( \frac{p_z}{p^\circ} \right) \right) = -3 - (-7) = 4 \] The change in \( \frac{10^4}{T} \) is:
\[ \Delta \left( \frac{10^4}{T} \right) = 12 - 10 = 2 \] So, the slope of the line is:
\[ m = \frac{4}{2} = 2 \] Step 3: Applying the slope to the formula
Now, we can use the relationship between the slope and \( \Delta H^{0} \):
\[ \text{Slope} = -\frac{\Delta H^{0}}{R} \] Substituting the slope and the value of \( R \) (8314 J/molΒ·K):
\[ 2 = -\frac{\Delta H^{0}}{8314} \] Solving for \( \Delta H^{0} \):
\[ \Delta H^{0} = -2 \times 8314 = -16628 \, \text{J/mol} \] Step 4: Calculating \( \Delta G^{0} \) at \( T = 1000 \, \text{K} \)
Using the equation for \( \Delta G^{0} \):
\[ \Delta G^{0} = -RT \ln K \] At \( T = 1000 \, \text{K} \), from the graph:
\[ \ln \left( \frac{p_z}{p^\circ} \right) = -3 \] Thus:
\[ \Delta G^{0} = -8314 \times 1000 \times (-3) = 24942000 \, \text{J/mol} = 24942 \, \text{kJ/mol} \] Step 5: Using the Gibbs Free Energy equation
Using the equation \( \Delta G^{0} = \Delta H^{0} - T \Delta S^{0} \), substitute known values:
\[ 24942 = -16628 - 1000 \times \Delta S^{0} \]
Step 6: Conclusion
The value of $\Delta S^{0}$ (in $J\, K ^{-1} mol ^{-1}$ ) for the given reaction, at $1000\, K$ is 141.34
Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant
- For the reaction $ N_2 + 3H_2 \rightleftharpoons 2NH_3 $, if initially 1 mole of $ N_2 $ and 3 moles of $ H_2 $ are taken and at equilibrium 0.4 moles of $ NH_3 $ are formed, find the equilibrium concentration of $ H_2 $.
- BITSAT - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- For the reaction \( \mathrm{N_2} + 3\mathrm{H_2} \rightleftharpoons 2\mathrm{NH_3} \), the equilibrium constant \(K_c\) is 0.5 at a certain temperature. If initially, 1 mole of \(\mathrm{N_2}\) and 3 moles of \(\mathrm{H_2}\) are placed in a 1 L container, what is the equilibrium concentration of \(\mathrm{NH_3}\)?
- BITSAT - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
The equilibrium constant for decomposition of $ H_2O $ (g) $ H_2O(g) \rightleftharpoons H_2(g) + \frac{1}{2} O_2(g) \quad (\Delta G^\circ = 92.34 \, \text{kJ mol}^{-1}) $ is $ 8.0 \times 10^{-3} $ at 2300 K and total pressure at equilibrium is 1 bar. Under this condition, the degree of dissociation ($ \alpha $) of water is _____ $\times 10^{-2}$ (nearest integer value). [Assume $ \alpha $ is negligible with respect to 1]
- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- Given below are two statements:
Statement I: A catalyst cannot alter the equilibrium constant ($ K_c $) of the reaction, temperature remaining constant.
Statement II: A homogeneous catalyst can change the equilibrium composition of a system, temperature remaining constant.
In the light of the above statements, choose the correct answer from the options given below.- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- In the following system, $ PCl_5(g) \rightleftharpoons PCl_3(g) + Cl_2(g) $ at equilibrium, upon addition of xenon gas at constant T and p, the concentration of
- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
Questions Asked in JEE Advanced exam
A temperature difference can generate e.m.f. in some materials. Let $ S $ be the e.m.f. produced per unit temperature difference between the ends of a wire, $ \sigma $ the electrical conductivity and $ \kappa $ the thermal conductivity of the material of the wire. Taking $ M, L, T, I $ and $ K $ as dimensions of mass, length, time, current and temperature, respectively, the dimensional formula of the quantity $ Z = \frac{S^2 \sigma}{\kappa} $ is:
- JEE Advanced - 2025
- Dimensional Analysis
- Let $$ \alpha = \frac{1}{\sin 60^\circ \sin 61^\circ} + \frac{1}{\sin 62^\circ \sin 63^\circ} + \cdots + \frac{1}{\sin 118^\circ \sin 119^\circ}. $$ Then the value of $$ \left( \frac{\csc 1^\circ}{\alpha} \right)^2 $$ is \rule{1cm}{0.15mm}.
- JEE Advanced - 2025
- Some Applications of Trigonometry
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- Consider the vectors $$ \vec{x} = \hat{i} + 2\hat{j} + 3\hat{k},\quad \vec{y} = 2\hat{i} + 3\hat{j} + \hat{k},\quad \vec{z} = 3\hat{i} + \hat{j} + 2\hat{k}. $$ For two distinct positive real numbers $ \alpha $ and $ \beta $, define $$ \vec{X} = \alpha \vec{x} + \beta \vec{y} - \vec{z},\quad \vec{Y} = \alpha \vec{y} + \beta \vec{z} - \vec{x},\quad \vec{Z} = \alpha \vec{z} + \beta \vec{x} - \vec{y}. $$ If the vectors $ \vec{X}, \vec{Y}, \vec{Z} $ lie in a plane, then the value of $ \alpha + \beta - 3 $ is ________.
Let $ y(x) $ be the solution of the differential equation $$ x^2 \frac{dy}{dx} + xy = x^2 + y^2, \quad x > \frac{1}{e}, $$ satisfying $ y(1) = 0 $. Then the value of $ 2 \cdot \frac{(y(e))^2}{y(e^2)} $ is ________.
- JEE Advanced - 2025
- Differential equations