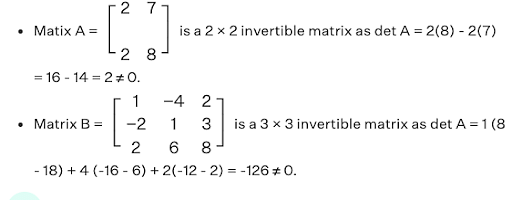Question:
Find the inverse of each of the matrices,if it exists.\(\begin{bmatrix}4&5\\3&4\end{bmatrix}\)
Find the inverse of each of the matrices,if it exists.\(\begin{bmatrix}4&5\\3&4\end{bmatrix}\)
Updated On: Sep 7, 2023
Hide Solution
Verified By Collegedunia
Solution and Explanation
The correct answer is \(A^{-1}=\begin{bmatrix}4&-5\\-3&4\end{bmatrix}\)
Let \(A=\begin{bmatrix}4&5\\3&4\end{bmatrix}\) We know that \(A = IA\)
so \(\begin{bmatrix}4&5\\3&4\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}\)
\(\implies \begin{bmatrix}1&1\\3&4\end{bmatrix}=\begin{bmatrix}1&-1\\0&1\end{bmatrix}A (R_1\rightarrow R_1-R_2)\)
\(\implies\begin{bmatrix}1&1\\0&1\end{bmatrix}=\begin{bmatrix}1&-1\\-3&4\end{bmatrix} A (R_2\rightarrow R_2-3R_1)\)
\(\implies\begin{bmatrix}1&1\\0&1\end{bmatrix}=\begin{bmatrix}4&-5\\3&4\end{bmatrix} A (R_1\rightarrow R_1-R_2)\)
therefore \(A^{-1}=\begin{bmatrix}4&-5\\-3&4\end{bmatrix}\)
Let \(A=\begin{bmatrix}4&5\\3&4\end{bmatrix}\) We know that \(A = IA\)
so \(\begin{bmatrix}4&5\\3&4\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}\)
\(\implies \begin{bmatrix}1&1\\3&4\end{bmatrix}=\begin{bmatrix}1&-1\\0&1\end{bmatrix}A (R_1\rightarrow R_1-R_2)\)
\(\implies\begin{bmatrix}1&1\\0&1\end{bmatrix}=\begin{bmatrix}1&-1\\-3&4\end{bmatrix} A (R_2\rightarrow R_2-3R_1)\)
\(\implies\begin{bmatrix}1&1\\0&1\end{bmatrix}=\begin{bmatrix}4&-5\\3&4\end{bmatrix} A (R_1\rightarrow R_1-R_2)\)
therefore \(A^{-1}=\begin{bmatrix}4&-5\\-3&4\end{bmatrix}\)
Was this answer helpful?
0
0
Top Questions on Matrices
- The number of $3\times2$ matrices $A$, which can be formed using the elements of the set $\{-2,-1,0,1,2\}$ such that the sum of all the diagonal elements of $A^{T}A$ is $5$, is
- If \[ X=\begin{bmatrix}x\\y\\z\end{bmatrix} \] is a solution of the system of equations $AX=B$, where \[ \text{adj }A= \begin{bmatrix} 4 & 2 & 2\\ -5 & 0 & 5\\ 1 & -2 & 3 \end{bmatrix} \quad \text{and} \quad B=\begin{bmatrix}4\\0\\2\end{bmatrix}, \] then $|x+y+z|$ is equal to
Let \[ f(x)=\int \frac{7x^{10}+9x^8}{(1+x^2+2x^9)^2}\,dx \] and $f(1)=\frac14$. Given that

- For the matrices \( A = \begin{bmatrix} 3 & -4 \\ 1 & -1 \end{bmatrix} \) and \( B = \begin{bmatrix} -29 & 49 \\ -13 & 18 \end{bmatrix} \), if \( (A^{15} + B) \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \), then among the following which one is true?}
- Let the relation \( R \) on the set \( M = \{1, 2, 3, \ldots, 16\} \) be given by \[ R = \{(x, y) : 4y = 5x - 3,\; x, y \in M\}. \] Then the minimum number of elements required to be added in \( R \), in order to make the relation symmetric, is equal to
View More Questions
Questions Asked in CBSE CLASS XII exam
- Suppose, the value of Average Propensity to Consume (APC) is 0.8 and National Income is ₹ 4,000 crores, the value of saving would be ₹ ____ crores. (Choose the correct option to fill up the blank)
- CBSE CLASS XII - 2025
- Income and Employment
- Surface area of a balloon (spherical), when air is blown into it, increases at a rate of 5 mm²/s. When the radius of the balloon is 8 mm, find the rate at which the volume of the balloon is increasing.
- Two wires of the same material and the same radius have their lengths in the ratio 2:3. They are connected in parallel to a battery which supplies a current of 15 A. Find the current through the wires.
- CBSE CLASS XII - 2025
- Current electricity
- (a) Briefly explain Einstein’s photoelectric equation.
(b) Four metals with their work functions are listed below:
K = 2.3 eV, Na = 2.75 eV, Mo = 4.17 eV, Ni = 5.15 eV.
The radiation of wavelength 330 nm from a laser source placed 1 m away, falls on these metals.
Which of these metals will not show photoelectric emission?
What will happen if the laser source is brought closer to a distance of 50 cm?- CBSE CLASS XII - 2025
- Photoelectric Effect
- Differentiate $2\cos^2 x$ w.r.t. $\cos^2 x$.
- CBSE CLASS XII - 2025
- Derivatives
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.