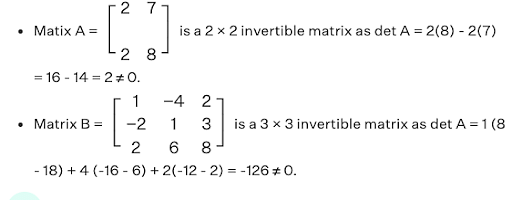Question:
Find the inverse of each of the matrices, if it exists.\(\begin{bmatrix}2&5\\1&3\end{bmatrix}\)
Find the inverse of each of the matrices, if it exists.\(\begin{bmatrix}2&5\\1&3\end{bmatrix}\)
Updated On: Sep 7, 2023
Hide Solution
Verified By Collegedunia
Solution and Explanation
The correct answer is \(A^{-1}=\begin{bmatrix}3&-5\\-1&2\end{bmatrix}\)
Let A=\(\begin{bmatrix}2&5\\1&3\end{bmatrix}\) We know that \(A = IA\)
so \([\begin{bmatrix}2&5\\1&3\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}A\)
\(\implies\begin{bmatrix}1& \frac{5}{2}\\ 1&3\end{bmatrix}=\begin{bmatrix}\frac{1}{2}& 0\\ 0&1\end{bmatrix}A (R_1\rightarrow\frac{1}{2R_1})\)
\(\implies \begin{bmatrix}1& \frac{5}{2}\\ 0& \frac{1}{2}\end{bmatrix}]=\begin{bmatrix}\frac{1}{2}& 0\\ \frac{-1}{2}& 1\end{bmatrix}A (R_2\rightarrow R_2-R_1)\)
\(\implies\begin{bmatrix}1&0\\0&\frac{1}{2}\end{bmatrix}=\begin{bmatrix}3&-5\\ \frac{-1}{2}& 1\end{bmatrix}A (R_1\rightarrow R_2-5R_2)\)
\(\implies\begin{bmatrix}1&0\\0&1\end{bmatrix}=\begin{bmatrix}3&-5\\-1&2\end{bmatrix}A (R_2\rightarrow2R_2)\)
therefore \(A^{-1}=\begin{bmatrix}3&-5\\-1&2\end{bmatrix}\)
Let A=\(\begin{bmatrix}2&5\\1&3\end{bmatrix}\) We know that \(A = IA\)
so \([\begin{bmatrix}2&5\\1&3\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}A\)
\(\implies\begin{bmatrix}1& \frac{5}{2}\\ 1&3\end{bmatrix}=\begin{bmatrix}\frac{1}{2}& 0\\ 0&1\end{bmatrix}A (R_1\rightarrow\frac{1}{2R_1})\)
\(\implies \begin{bmatrix}1& \frac{5}{2}\\ 0& \frac{1}{2}\end{bmatrix}]=\begin{bmatrix}\frac{1}{2}& 0\\ \frac{-1}{2}& 1\end{bmatrix}A (R_2\rightarrow R_2-R_1)\)
\(\implies\begin{bmatrix}1&0\\0&\frac{1}{2}\end{bmatrix}=\begin{bmatrix}3&-5\\ \frac{-1}{2}& 1\end{bmatrix}A (R_1\rightarrow R_2-5R_2)\)
\(\implies\begin{bmatrix}1&0\\0&1\end{bmatrix}=\begin{bmatrix}3&-5\\-1&2\end{bmatrix}A (R_2\rightarrow2R_2)\)
therefore \(A^{-1}=\begin{bmatrix}3&-5\\-1&2\end{bmatrix}\)
Was this answer helpful?
0
0
Top Questions on Matrices
- If $$ A = \begin{pmatrix} 2 & 3 \\ 1 & k \end{pmatrix} $$ and $\det(A) = 7$, find the value of $ k $.
- Find x, y, z if
\[ \begin{bmatrix} 5 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} 0 & 1 & -2 \\ 1 & -2 & 3 \\ -1 & 1 & 1 \end{bmatrix} \begin{bmatrix} x-1 \\ y+1 \\ 2z \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}. \] - For all \( n \in \mathbb{N} \), if \( 1^3 + 2^3 + 3^3 + \cdots + n^3>x \), then a value of \( x \) among the following is:
- If $A$ and $B$ are two square matrices each of order 3 with $|A| = 3$ and $|B| = 5$, then $|2AB|$ is:
- If \( \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} \) is a scalar matrix, then \( x^y \) is equal to:
View More Questions
Questions Asked in CBSE CLASS XII exam
- Emily, Flora and Ginni entered into a partnership on 1st October, 2023 with capitals of ₹ 10,00,000 each. The partnership deed provided for interest on capital at 10% p.a. The firm earned a net profit of ₹ 7,50,000 for the year ended 31st March, 2024. The amount of profit transferred to Emily’s capital account was :
- CBSE CLASS XII - 2025
- Partnership Accounts
- "The Government had launched Incredible India Campaign to promote tourism in various parts of the country."
Elaborate the impact of Incredible India Campaign on foreign exchange reserves and Balance of Payment of India.- CBSE CLASS XII - 2025
- Balance of payments (BOP)
- Ajanta Ltd. purchased machinery worth Rs 36,00,000 from Sujata Ltd. Ajanta Ltd. paid half the amount to Sujata Ltd. through a bank draft and the balance by issuing 8 debentures of Rs 100 each at a discount of 10.
Pass the necessary journal entries in the books of Ajanta Ltd. for the above transactions.- CBSE CLASS XII - 2025
- Debentures
- From the following information obtained from the books of KVK Ltd., calculate Net Assets Turnover Ratio and Debt Equity Ratio:
Information Table
Information Amount (₹) Preference Share Capital 8,00,000 Equity Share Capital 12,00,000 General Reserve 2,00,000 Balance in Statement of Profit and Loss 6,00,000 15% Debentures 4,00,000 12% Loan 4,00,000 Revenue from Operations 72,00,000 - CBSE CLASS XII - 2025
- Financial Statement Analysis
- Zaina, Yash and Kiran were partners in a firm sharing profits and losses in the ratio of 2 : 2 : 1. Zaina died on 1st July, 2024. As per the partnership deed, Zaina’s share of profit or loss till the date of her death was to be calculated on the basis of sales. Sales for the year ended 31st March, 2024 amounted to ₹ 4,00,000 and that from 1st April to 30th June, 2024 was ₹ 1,50,000. The profit for the year ending 31st March, 2024 was ₹ 1,00,000. Calculate Zaina’s share of profit in the firm till the date of her death and pass necessary journal entry for the same.
- CBSE CLASS XII - 2025
- Retirement and Death of a Partner
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.