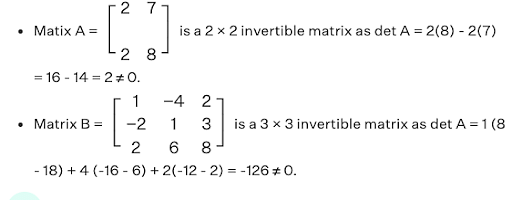Find the inverse of each of the matrices,if it exists \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)
Solution and Explanation
Let A=\(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)
We know that\(A = IA\)
\(\therefore\) \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)= \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) A
⇒ \(\begin{bmatrix} 1 & \frac12 \\ 7 & 4 \end{bmatrix}\)=\(\begin{bmatrix} \frac12 & 0 \\ 0 & 1 \end{bmatrix}\)A (R1\(→\) \(\frac{1}{2}R_1\))
⇒\(\begin{bmatrix} 1 & \frac12 \\ 0 & \frac12 \end{bmatrix}\)=\(\begin{bmatrix} \frac12 &0\\ -\frac72 & 1 \end{bmatrix}\)A (R2→R2-7R1)
⇒ \(\begin{bmatrix} 1 & 0 \\ 0 & \frac12 \end{bmatrix}\)=\(\begin{bmatrix} 4 & -1 \\ -\frac72 & 1 \end{bmatrix}\)A (R1->R1-R2)
⇒ \(\begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 4 & -1 \\ -7 & 2 \end{bmatrix}\)A (R2->2R2)
\(\therefore\) A-1=\(\begin{bmatrix} 4 & -1 \\ -7 & 2 \end{bmatrix}\)
Top Questions on Matrices
- For all \( n \in \mathbb{N} \), if \( 1^3 + 2^3 + 3^3 + \cdots + n^3>x \), then a value of \( x \) among the following is:
- If $A$ and $B$ are two square matrices each of order 3 with $|A| = 3$ and $|B| = 5$, then $|2AB|$ is:
- If \( \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} \) is a scalar matrix, then \( x^y \) is equal to:
- If $M$ and $N$ are square matrices of order 3 such that $\det(M) = m$ and $MN = mI$, then $\det(N)$ is equal to :
- Find the determinant of the matrix \( A = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} \).
Questions Asked in CBSE CLASS XII exam
- Find: \[ \int \frac{2x}{(x^2 + 3)(x^2 - 5)} \, dx \]
- CBSE CLASS XII - 2025
- Integration
- If \( \int \frac{1}{2x^2} \, dx = k \cdot 2x + C \), then \( k \) is equal to:
- CBSE CLASS XII - 2025
- Integration
- Two dice are thrown. Defined are the following two events A and B: \[ A = \{(x, y) : x + y = 9\}, \quad B = \{(x, y) : x \neq 3\}, \] where \( (x, y) \) denote a point in the sample space. Check if events \( A \) and \( B \) are independent or mutually exclusive.
- CBSE CLASS XII - 2025
- Probability
- Find the least value of ‘a’ so that $f(x) = 2x^2 - ax + 3$ is an increasing function on $[2, 4]$.
- CBSE CLASS XII - 2025
- Functions
- Light consisting of two wavelengths 600 nm and 480 nm is used to obtain interference fringes in a double slit experiment. The screen is placed 1.0 m away from slits which are 1.0 mm apart. (i) Calculate the distance of the third bright fringe on the screen from the central maximum for wavelength 600 nm.
- CBSE CLASS XII - 2025
- electrostatic potential and capacitance
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.