Find the coordinates of the point where the line through A (9, 4 , 1) and B (5, 1, 6) crosses X axis ?
Find the coordinates of the point where the line through A (9, 4 , 1) and B (5, 1, 6) crosses X axis ?
Solution and Explanation
To find the coordinates of the point where the line through points A(9, 4, 1) and B(5, 1, 6) crosses the X-axis, we need to determine the value of the X-coordinate when the Y and Z coordinates are both zero.
Step 1: Find the direction vector of the line:
The direction vector of the line can be found by subtracting the coordinates of B from A:
\[
AB = [5 - 9, 1 - 4, 6 - 1] = [-4, -3, 5]
\]
Step 2: Write the parametric equations for the line:
Using the direction vector, we can write the parametric equations for the line as:
\[
x = 9 - 4t
\]
\[
y = 4 - 3t
\]
\[
z = 1 + 5t
\]
where \( t \) is a parameter representing the position along the line.
Step 3: Set \( y = 0 \) and \( z = 0 \) to find the intersection with the X-axis:
The line crosses the X-axis when both \( y \) and \( z \) are zero. So, we solve the following system of equations:
\[
4 - 3t = 0
\]
\[
1 + 5t = 0
\]
Step 4: Solve the system of equations:
From the first equation, solve for \( t \):
\[
4 - 3t = 0 \quad \Rightarrow \quad t = \frac{4}{3}
\]
From the second equation, solve for \( t \):
\[
1 + 5t = 0 \quad \Rightarrow \quad t = -\frac{1}{5}
\]
Step 5: Determine the correct value of \( t \):
We have two different values of \( t \), \( t = \frac{4}{3} \) and \( t = -\frac{1}{5} \). However, since we are looking for the point where the line intersects the X-axis, we only need the value of \( t \) that gives us the X-coordinate. Substituting the correct value of \( t = \frac{4}{3} \) into the parametric equation for \( x \), we get:
\[
x = 9 - 4\left(\frac{4}{3}\right) = 9 - \frac{16}{3} = \frac{27}{3} - \frac{16}{3} = \frac{11}{3}
\]
Step 6: Final Answer:
Therefore, the coordinates of the point where the line crosses the X-axis are approximately:
\[
\left(\frac{11}{3}, 0, 0\right)
\]
which simplifies to:
\[
(3.67, 0, 0)
\]
Top Questions on introduction to three dimensional geometry
- If the 4th, 10th, and 16th terms of a G.P. are \(x\), \(y\), and \(z\) respectively, then
- KCET - 2025
- Mathematics
- introduction to three dimensional geometry
- The number of diagonals that can be drawn in an octagon is:
- KCET - 2025
- Mathematics
- introduction to three dimensional geometry
- The equation of the line through the point \( (0, 1, 2) \) and perpendicular to the line \[ \frac{x - 1}{2} = \frac{y + 1}{3} = \frac{z - 1}{-2} \] is:
- KCET - 2025
- Mathematics
- introduction to three dimensional geometry
- Let \( \vec{a}, \vec{b}, \vec{c} \) be three vectors. The angle between \( \vec{a} \) and \( \vec{b} \) is \( 30^\circ \), the angle between \( \vec{a} \) and \( \vec{b} + \vec{c} \) is \( 45^\circ \). If \( |\vec{b}| = \sqrt{6} \) and \( |\vec{c}| = 2\sqrt{2} \), then \( |\vec{b} + \vec{c}| \) is:
- KEAM - 2024
- Mathematics
- introduction to three dimensional geometry
- Let \[ f(x) = \frac{|5 - x|(x + 5)}{\tan(x - 5)} \quad {for} \quad x \neq 5. \] Then \[ \lim_{x \to 5} f(x) { is equal to:} \]
- KEAM - 2024
- Mathematics
- introduction to three dimensional geometry
Questions Asked in MHT CET exam
- Evaluate the integral: \[ \int \frac{\sqrt{\tan x}}{\sin x \cos x} \, dx \]
- MHT CET - 2025
- Integration
- Solve the system of equations: \[ x + y = 10 \] \[ 3x - y = 5 \]
- MHT CET - 2025
- linear inequalities
- Population of Town A and B was 20,000 in 1985. In 1989, the population of Town A was 25,000, and Town B had 28,000. What will be the difference in population between the two towns in 1993?
- MHT CET - 2025
- Population Growth Calculation
- Which of the following solutions will show highest freezing point depression?
- MHT CET - 2025
- Colligative Properties
- Given the formula for depression of freezing point: \[ \Delta T_f = K_f \cdot m \] where \( \Delta T_f \) is the depression of freezing point, \( K_f \) is the freezing point depression constant, and \( m \) is the molality, calculate the value of \( m \).
- MHT CET - 2025
- Colligative Properties
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
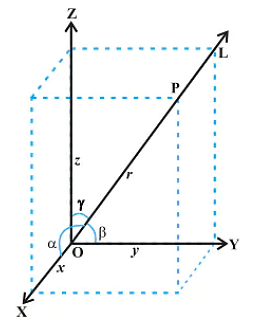
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.