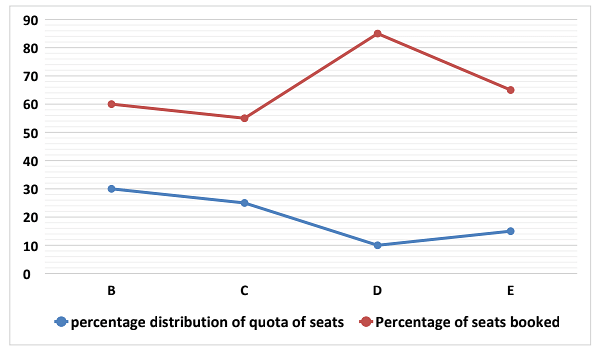
A train ‘T’ starts from station ‘A’ for station ‘F’. In between stations ‘A’ and ‘F’, there are four intermediate stations ‘B’, ‘C’, ‘D’ and ‘E’, respectively, in the same order. Stations ‘A’, ‘B’, ‘C’, ‘D’ and ‘E’ has quota for seats booking. The line graph given below represents the percentage distribution of quota of seats given to the respective stations out of total number of seats in the train and percentage of seats booked out of them.
The table below represents the total vacant seats in the train after leaving the respective stations.
| Stations | Total vacant seats |
| B | 562 |
| C | 494 |
| D | 514 |
| E | 472 |
Note:
1. When train left station A, number of vacant seats was 688 and 30% of quota seats of station A were not booked.
2. A seat can be booked for only one person from the respective stations and the same person can board the train from that station.
3. All the persons who booked tickets boarded the train.
Find the ratio of number of passengers who boarded the train at station ‘B’ and number of passengers who de-boarded the train at station ‘D’.
- 13:9
- 12:7
- 18:11
- 10:3
The Correct Option is C
Solution and Explanation
The correct option is (C): 18:11.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required ratio = 144:88 = 18:11.
boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required ratio = 144:88 = 18:11.
Out of total number of passengers in the train after it left station ‘C’, 50% were females. Find the difference between number of males in the train after it left station ‘C’ and number of passengers who deboarded the train at station ‘B’.
- 135
- 215
- 123
- 141
The Correct Option is A
Solution and Explanation
The correct option is (A): 135.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = \(\frac{688}{0.86} \)= 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required difference = (0.5 × 306) – 18 = 153 – 18 = 135.
rded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required difference = (0.5 × 306) – 18 = 153 – 18 = 135.
Find the average of the number of passengers who de-boarded the train at stations ‘E’ and ‘F’ together.
- 212
- 272
- 192
- 182
The Correct Option is D
Solution and Explanation
The correct option is (D): 182.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required average = {\(\frac{(36 + 328)}{2}\)} = 182.
After the train left station ‘D’, each passenger has 3 bags with him.
Find the total number of bags with the passengers in the train after it left
station ‘D’.
Find the total number of bags with the passengers in the train after it left
station ‘D’.
- 766
- 512
- 858
- 912
The Correct Option is C
Solution and Explanation
The correct option is (C): 858.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required number of bags = 286 × 3 = 858.
If at each station, 75% of total number of passengers who boarded the train were males then find the sum of number of all the females who boarded the train at given stations.
- 194
- 148
- 156
- 128
The Correct Option is D
Solution and Explanation
The correct option is (D): 128.
Let total number of seats in the train be ‘x’
Percentage of quota of seats given to station ‘A’ = 100 – (30 + 25 + 10 +15) = 20%
So, number of seats available for booking in station A = 0.2x
Therefore, number of seats booked station A = 70% of 0.2x = 0.14x
So, x – 688 = 0.14x
Or, 0.86x = 688
Or, x = 688/0.86 = 800
The table below shows the information about number of seats available, booked and not booked for respective stations.
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 20% of 800 = 160 | 70% of 160 =112 | 48 |
| B | 30% of 800 = 240 | 60% of 240 =144 | 96 |
| C | 25% of 800 = 200 | 55% of 200 =110 | 90 |
| D | 10% of 800 = 80 | 85% of 80 = 68 | 12 |
| E | 15% of 800 = 120 | 65% of 120 =78 | 42 |
So, number of passengers in the train after leaving station ‘B’ = 800 –562 = 238
Number of passengers who boarded from station ‘A’ = 112
Number of passengers who boarded from station ‘B’ = 144
Therefore, number of passengers in the train after leaving station ‘B’ =Number of passengers who boarded from station ‘A’ + Number of
passengers who boarded from station ‘B’ – number of passengers who de-boarded at station ‘B’
So, 238 = 112 + 144 – number of passengers who de-boarded at station ‘B’
Or, number of passengers who de-boarded at station ‘B’ = 256 – 238 =18
Similarly,
| Station | Number of seats which is available for booking | Number of seats which were booked | Number of seats which were not booked |
| A | 112 | 112 | - |
| B | 144 | 238 | 18 |
| C | 110 | 306 | 42 |
| D | 68 | 286 | 88 |
| E | 78 | 328 | 36 |
| F | - | - | 328 |
Required number of females = 0.25 × (112 + 144 + 110 + 68 + 78) =128.
Top Questions on Data Interpretation
- In a code language, 'TIGER' is written as 'JUISF'. How will 'EQUAL' be written in that language?
- VITEEE - 2025
- General Aptitude
- Data Interpretation
- Eight employees of an organization have been rated on a scale of 1 to 50 for their performance. All ratings are integers. The overall average rating of the eight employees is 30. While the five employees with the highest ratings average 38, the five employees with the lowest ratings average 25. Which of the following, about the ratings obtained by the eight employees, is DEFINITELY FALSE?
- XAT - 2025
- Quantitative Ability and Data Interpretation
- Data Interpretation
The plots below depict and compare the average monthly incomes (in Rs. ’000) of males and females in ten cities of India in the years 2005 and 2015. The ten cities, marked A-J in the records, are of different population sizes. For a fair comparison, to adjust for inflation, incomes for both the periods are scaled to 2025 prices. Each red dot represents the average monthly income of females in a particular city in a particular year, while each blue dot represents the average monthly income of males in a particular city in a particular year. The gender gap for a city, for a particular year, is defined as the absolute value of the average monthly income of males, minus the average monthly income of females, in that year.
- XAT - 2025
- Quantitative Ability and Data Interpretation
- Data Interpretation
- Among the following, the correct picture representation of the number of school teachers in Delhi is:
- TG EDCET - 2025
- Mathematics
- Data Interpretation
A bar graph shows the number of students in 5 departments of a college. If the average number of students is 240 and the number of students in the Science department is 320, how many students are there in total in the other four departments?
- CUET (UG) - 2025
- General Aptitude
- Data Interpretation
Questions Asked in CAT exam
- If \(x\) and \(y\) are real numbers such that \(4x^2 + 4y^2 - 4xy - 6y + 3 = 0\), then the value of \((4x + 5y)\) is
- CAT - 2024
- Linear & Quadratic Equations
- Two points A and B are 45 km apart. Anil started from A. Sunil started from B. They met each other after 1 hour 30 mins. and after meeting, they continued towards their destinations. Time taken by Anil to reach Point B was 1 hr 15 mins more than the time taken by Sunil to reach point A. Find speed of Anil
- CAT - 2024
- Time, Speed and Distance
- The sum of all four-digit numbers that can be formed with the distinct non-zero digits $a$, $b$, $c$, and $d$, with each digit appearing exactly once in every number, is $153310 + n$, where $n$ is a single digit natural number. Then, the value of $(a + b + c + d)$ is ?
- CAT - 2024
- Permutations and Combinations
- Let $x$, $y$, and $z$ be real numbers satisfying
\(4(x^2 + y^2 + z^2) = a,\)
\(4(x - y - z) = 3 + a.\)
Then $a$ equals ?- CAT - 2024
- Algebra
- The sum of all real values of $k$ for which $(\frac{1}{8})^k \times (\frac{1}{32768})^{\frac{4}{3}} = \frac{1}{8} \times (\frac{1}{32768})^{\frac{k}{3}}$ is
- CAT - 2024
- Logarithms