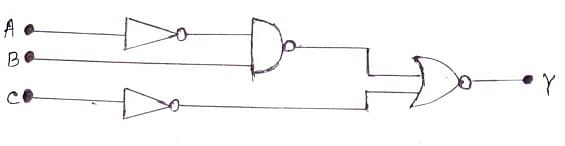
Consider the logic circuit with inputs A,B,C, and output Y. How many combinations of A, B and C give the output Y=0?

Consider the logic circuit with inputs A,B,C, and output Y. How many combinations of A, B and C give the output Y=0?
- 8
- 5
- 7
- 1
The Correct Option is C
Approach Solution - 1
In a logic circuit with inputs A, B, and C, each input can take values 0 or 1. Since there are three binary inputs, the total number of input combinations is:
$2^3 = 8$
We are interested in the number of combinations that result in output $Y = 0$.
From the logic of the circuit, the combinations that result in $Y = 0$ are:
- $A = 0$, $B = 0$, $C = 0$
- $A = 0$, $B = 0$, $C = 1$
- $A = 0$, $B = 1$, $C = 0$
- $A = 1$, $B = 0$, $C = 0$
- $A = 0$, $B = 1$, $C = 1$
- $A = 1$, $B = 0$, $C = 1$
- $A = 1$, $B = 1$, $C = 0$
So, the number of combinations giving output $Y = 0$ is 7.
Correct option: (C): 7
Approach Solution -2
Given Boolean Expression:
$D = \overline{\overline{(A + B)} \cdot C}$
Using De Morgan’s Law: $\overline{P \cdot Q} = \overline{P} + \overline{Q}$
So, this becomes:
$D = \overline{\overline{(A + B)} + \overline{C}}$
Case 1: $A = 0$, $B = 0$, $C = 0$
- $A + B = 0 + 0 = 0$
- $\overline{(A + B)} = \overline{0} = 1$
- $\overline{C} = \overline{0} = 1$
- Now: $D = \overline{1 + 1} = \overline{1} = 0$
Case 2: $A = 1$, $B = 1$, $C = 0$
- $A + B = 1 + 1 = 1$
- $\overline{(A + B)} = \overline{1} = 0$
- $\overline{C} = \overline{0} = 1$
- Now: $D = \overline{0 + 1} = \overline{1} = 0$
Case 3: $A = 0$, $B = 1$, $C = 1$
- $A + B = 0 + 1 = 1$
- $\overline{(A + B)} = \overline{1} = 0$
- $\overline{C} = \overline{1} = 0$
- Now: $D = \overline{0 + 0} = \overline{0} = 1$
Conclusion:
The output $D$ depends on the specific values of $A$, $B$, and $C$. The expression simplifies using De Morgan's Law, and for each combination, we calculate step by step. As shown above, when the sum inside is 1, and $\overline{C}$ is also 1, the result becomes 0.
Top Questions on Logic gates
Consider the following logic circuit.

The output is Y = 0 when :- JEE Main - 2025
- Physics
- Logic gates
- The radiation pressure exerted by a 450 W light source on a perfectly reflecting surface placed at 2m away from it, is :
- JEE Main - 2025
- Physics
- Logic gates
- Choose the correct logic circuit for the given truth table having inputs A and B.

- JEE Main - 2025
- Physics
- Logic gates
The logic gate equivalent to the combination of logic gates shown in the figure is

- AP EAPCET - 2025
- Physics
- Logic gates
The output (Y) of the given logic implementation is similar to the output of an/a …………. gate.

- NEET (UG) - 2025
- Physics
- Logic gates
Questions Asked in WBJEE exam
- The variation of displacement with time of a simple harmonic motion (SHM) for a particle of mass \( m \) is represented by: \[ y = 2 \sin \left( \frac{\pi}{2} + \phi \right) \, \text{cm} \] The maximum acceleration of the particle is:
- WBJEE - 2025
- simple harmonic motion
- Ruma reached the metro station and found that the escalator was not working. She walked up the stationary escalator with velocity \( v_1 \) in time \( t_1 \). On another day, if she remains stationary on the escalator moving with velocity \( v_2 \), the escalator takes her up in time \( t_2 \). The time taken by her to walk up with velocity \( v_1 \) on the moving escalator will be:
- WBJEE - 2025
- Relative Motion
- A force \( \mathbf{F} = ai + bj + ck \) is acting on a body of mass \( m \). The body was initially at rest at the origin. The co-ordinates of the body after time \( t \) will be:
- WBJEE - 2025
- Newtons Laws of Motion
A quantity \( X \) is given by: \[ X = \frac{\epsilon_0 L \Delta V}{\Delta t} \] where:
- \( \epsilon_0 \) is the permittivity of free space,
- \( L \) is the length,
- \( \Delta V \) is the potential difference,
- \( \Delta t \) is the time interval.
The dimension of \( X \) is the same as that of:- WBJEE - 2025
- Dimensional Analysis
- If \( {}^9P_3 + 5 \cdot {}^9P_4 = {}^{10}P_r \), then the value of \( 'r' \) is:
- WBJEE - 2025
- permutations and combinations
Concepts Used:
Logic Gates
AND Gate
It is the gate, where a circuit performs an AND operation. It has n number of input where (n >= 2) and one output.
OR Gate
It is the gate, where a circuit performs an OR operation. It has n number of input where (n >= 2) and one output.
NOT Gate
An inverter is also called NOT Gate. It has one input and one output where the input is A and the output is Y.
NAND Gate
A NAND operation is also called a NOT-AND operation. It has n number of input where (n >= 2) and one output.
NOR Gate
A NOR operation is also called a NOT-OR operation. It has n number of input where (n >= 2) and one output.
XOR Gate
XOR or Ex-OR gate is a specific type of gate that can be used in the half adder, full adder, and subtractor.
XNOR Gate
XNOR gate is a specific type of gate, which can be used in the half adder, full adder, and subtractor. The exclusive-NOR gate is flattened as an EX-NOR gate or sometimes as an X-NOR gate. It has n number of input (n >= 2) and one output.