Question:
Choose the correct mirror image of the following:
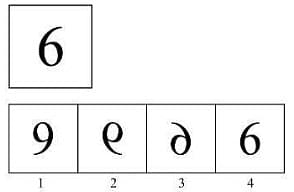
Choose the correct mirror image of the following:
Updated On: May 11, 2025
- 1
- 2
- 3
- 4
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
To solve the problem of identifying the correct mirror image of a figure, it is crucial to understand the concept of a mirror image. A mirror image reverses the original figure as if it is reflecting across a vertical axis (the mirror line). Here are the steps to determine the correct mirror image:
- Analyze the given figure: Observe the elements of the original figure carefully. Identify distinctive features that will be reversed in the mirror image.
- Determine the transformations: In a mirror image, left and right are swapped. Any text, pattern, or orientation will appear flipped when compared to the original.
- Compare with options: Examine each option provided to find the one that correctly mimics the properties of a mirror image.
- Verify environmental factors: Ensure that all patterns, angles, and relative positions are mirrored accurately.
Upon comparison, option 3 reflects the correct mirror image of the original figure, confirming it matches all reversed elements accurately with no discrepancies. Therefore, the correct answer is option 3.
Was this answer helpful?
0
0
Top Questions on Age
Let $\Sigma = \{a, b, c\}$. For $x \in \Sigma^*$, and $\alpha \in \Sigma$, let $\#\alpha(x)$ denote the number of occurrences of $\alpha$ in $x$. Which one or more of the following option(s) define(s) regular language(s)?
- Which ONE of the following languages is accepted by a deterministic pushdown automaton?
- Arjun is twice as old as Shreya. Five years ago, his age was three times Shreya's age. Find the sum of their present ages:
- A child was born on 13th January 1976 which was a Tuesday. What day of the week will be the childs birth day in the year 1986?
- Beena got married 8 years ago. Today, her age is \(\frac {11}{4}\) times her age at the time of marriage. If her daughter‘s age is \(\frac {1}{10}\) times her age, then her daughter‘s age is:
View More Questions
Questions Asked in CUET exam
Match List-I with List-II
\[\begin{array}{|l|l|} \hline \text{List-I (Physical Quantity)} & \text{List-II (Units)} \\ \hline \text{(A) Magnetic field} & \text{(I) J T\(^{-1}\)} \\ \hline \text{(B) Magnetic moment} & \text{(II) T m A\(^{-1}\)} \\ \hline \text{(C) Pole strength} & \text{(III) J T\(^{-1}\) m\(^{-1}\)} \\ \hline \text{(D) Permeability of free space} & \text{(IV) Wb m\(^{-2}\)} \\ \hline \end{array}\]Choose the correct answer from the options given below:
- CUET (UG) - 2025
- Magnetism
- A proton accelerated through a potential difference of V volts has a de-Broglie wavelength \(\lambda\) associated with it. In order to get the same wavelength associated with an \(\alpha\)-particle, the required accelerating potential is
- CUET (UG) - 2025
- de broglie hypothesis
- In the following nuclear reaction, \(^1_0\text{n} + ^{235}_{92}\text{U} \rightarrow ^{140}_{54}\text{Xe} + ^b_a\text{Sr} + 2(^1_0\text{n})\) we have
- CUET (UG) - 2025
- Fusion and Fission
- On connecting a device X in a series circuit with a battery and a resistor, a current passes through the circuit. On reversing the polarity of the battery, the current in the circuit drops to almost zero. The device X may be a
- CUET (UG) - 2025
- PN Junction Diode
- Which of the following statement(s) is/are true for p-type semiconductors?
(A) Holes are minority carriers and pentavalent atoms are the dopants.
(B) Electrons are majority carriers and trivalent atoms are the dopants.
(C) Holes are majority carriers and trivalent atoms are the dopants.
(D) Electrons are minority carriers and pentavalent atoms are the dopants.
Choose the correct answer from the options given below:- CUET (UG) - 2025
- Semiconductor Materials
View More Questions