Question

A wide slab consisting of two media of refractive indices $n_{1}$ and $n_{2}$ is placed in air as shown in the figure. A ray of light is incident from medium $n _{1}$ to $n _{2}$ at an angle $\theta$, where $\sin \theta$ is slightly larger than $\frac1 { n _{1}}$. Take refractive index of air as $1$.Which of the following statement(s) is(are) correct?

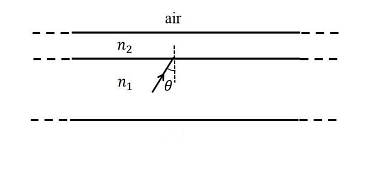
• A. The light ray enters air if $n_{2}=n_{1}$
• B. The light ray is finally reflected back into the medium of refractive index $n _{1}$ if $n _{2}< n _{1}$
• C. The light ray is finally reflected back into the medium of refractive index $n_{1}$ if $n_{2}>n_{1}$
• D. The light ray is reflected back into the medium of refractive index $n_{1}$ if $n_{2}=1$

Answer 1

The Correct Option is B, C, D

Step 1: Understanding the given inequality
The inequality given is:
\( \sin(\theta) > \frac{1}{n_1} \) … (i)
This inequality is derived from Snell's law for refraction, where \( n_1 \) is the refractive index of the initial medium and \( \theta \) is the angle of incidence. The equation suggests that the sine of the angle of incidence is greater than \( \frac{1}{n_1} \), implying that the angle of incidence is such that refraction cannot occur into the second medium under certain conditions.
Step 2: Applying Snell's law
Snell’s law relates the refractive indices and the angles of incidence and refraction:
\[ n_1 \sin(\theta) = n_2 \sin(r) \] where:
- \( n_1 \) is the refractive index of the first medium,
- \( \theta \) is the angle of incidence,
- \( n_2 \) is the refractive index of the second medium,
- \( r \) is the angle of refraction.
From equation (ii), we have \( n_1 \sin(\theta) = 1 \times \sin(r) \), which simplifies to:
\[ n_1 \sin(\theta) = \sin(r) \] Step 3: Identifying the condition for refraction
If we substitute the first inequality from equation (i), we get:
\[ \sin(r) > 1 \] But \( \sin(r) \) cannot be greater than 1 because the sine of any angle is always between -1 and 1.
Therefore, refraction into the second medium (air) is not possible in this case.
Step 4: Considering total internal reflection
When refraction is not possible, the light ray will undergo total internal reflection. This occurs when the refractive index of the second medium \( n_2 \) is smaller than that of the first medium \( n_1 \), leading to the light ray being reflected back into the first medium.
Step 5: Analyzing the correct options
The correct options based on the reasoning are:
(B): The light ray is finally reflected back into the medium of refractive index \( n_1 \) if \( n_2 < n_1 \).
(C): The light ray is finally reflected back into the medium of refractive index \( n_1 \) if \( n_2 > n_1 \).
(D): The light ray is reflected back into the medium of refractive index \( n_1 \) if \( n_2 = 1 \).