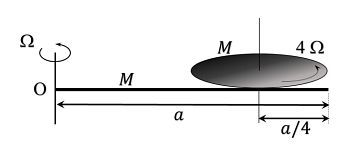
A thin rod of mass $M$ and length $a$ is free to rotate in horizontal plane about a fixed vertical axis passing through point $O$. A thin circular disc of mass $M$ and of radius $a / 4$ is pivoted on this rod with its center at a distance $a / 4$ from the free end so that it can rotate freely about its vertical axis, as shown in the figure. Assume that both the rod and the disc have uniform density and they remain horizontal during the motion. An outside stationary observer finds the rod rotating with an angular velocity $\Omega$ and the disc rotating about its vertical axis with angular velocity $4\, \Omega$. The total angular momentum of the system about the point $O$ is $\left(\frac{ Ma ^{2} \Omega}{48}\right) n$. The value of $n$ is ______

Correct Answer: 49
Solution and Explanation
Given:
- Thin rod of mass M and length a rotating about point O with angular velocity Ω
- A thin disc of mass M and radius a/4 is attached at distance a/4 from the free end of the rod
- The disc is rotating with angular velocity 4Ω about its own vertical axis
- We are to find the total angular momentum of the system about point O in terms of (M a² Ω / 48)·n
Step 1: Angular momentum of the rod about point O
Moment of inertia of thin rod about one end (axis perpendicular to length):
Irod = (1/3) M a²
Angular momentum = I × Ω = (1/3) M a² Ω
Step 2: Angular momentum of the disc
Total angular momentum of the disc has two parts:
- Due to rotation of the disc's center about O:
- Due to spinning of the disc about its own axis:
Total disc angular momentum = (9/16 + 1/8) M a² Ω
Convert to common denominator: (9/16 + 2/16) = 11/16
So, Ldisc = (11/16) M a² Ω
Step 3: Total angular momentum about O
Ltotal = Lrod + Ldisc = (1/3) M a² Ω + (11/16) M a² Ω
Take LCM:
(1/3) = (16/48), (11/16) = (33/48)
⇒ Ltotal = (16 + 33)/48 M a² Ω = (49/48) M a² Ω
Final Answer: n = 49
Top Questions on Rotational motion
- A solid sphere of mass 2 kg and radius 0.5 m rolls without slipping down an inclined plane of height 3 m. What is its speed at the bottom? (Take \( g = 9.8\, \text{m/s}^2 \))
- BITSAT - 2025
- Physics
- Rotational motion
- Moment of inertia of a rod of mass \( M \) and length \( L \) about an axis passing through its center and normal to its length is \( \alpha \). Now the rod is cut into two equal parts and these parts are joined symmetrically to form a cross shape. Moment of inertia of cross about an axis passing through its center and normal to the plane containing cross is:
- JEE Main - 2025
- Physics
- Rotational motion
A wheel of radius $ 0.2 \, \text{m} $ rotates freely about its center when a string that is wrapped over its rim is pulled by a force of $ 10 \, \text{N} $. The established torque produces an angular acceleration of $ 2 \, \text{rad/s}^2 $. Moment of inertia of the wheel is............. kg m².
- JEE Main - 2025
- Physics
- Rotational motion
- A thin spherical shell of radius \( 0.5 \, \text{m} \) and mass \( 2 \, \text{kg} \) is rotating about its axis of symmetry with an angular velocity of \( 10 \, \text{rad/s} \). What is its moment of inertia?
- MHT CET - 2025
- Physics
- Rotational motion
- A rod of linear mass density $ \lambda $ and length $ L $ is bent to form a ring of radius $ R $. Moment of inertia of the ring about any of its diameter is:
- JEE Main - 2025
- Physics
- Rotational motion
Questions Asked in JEE Advanced exam
As shown in the figures, a uniform rod $ OO' $ of length $ l $ is hinged at the point $ O $ and held in place vertically between two walls using two massless springs of the same spring constant. The springs are connected at the midpoint and at the top-end $ (O') $ of the rod, as shown in Fig. 1, and the rod is made to oscillate by a small angular displacement. The frequency of oscillation of the rod is $ f_1 $. On the other hand, if both the springs are connected at the midpoint of the rod, as shown in Fig. 2, and the rod is made to oscillate by a small angular displacement, then the frequency of oscillation is $ f_2 $. Ignoring gravity and assuming motion only in the plane of the diagram, the value of $\frac{f_1}{f_2}$ is:

- JEE Advanced - 2025
- Waves and Oscillations
The reaction sequence given below is carried out with 16 moles of X. The yield of the major product in each step is given below the product in parentheses. The amount (in grams) of S produced is ____.

Use: Atomic mass (in amu): H = 1, C = 12, O = 16, Br = 80- JEE Advanced - 2025
- Organic Chemistry
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
Concepts Used:
Rotational Motion
Rotational motion can be defined as the motion of an object around a circular path, in a fixed orbit.
Rotational Motion Examples:
The wheel or rotor of a motor, which appears in rotation motion problems, is a common example of the rotational motion of a rigid body.
Other examples:
- Moving by Bus
- Sailing of Boat
- Dog walking
- A person shaking the plant.
- A stone falls straight at the surface of the earth.
- Movement of a coin over a carrom board
Types of Motion involving Rotation:
- Rotation about a fixed axis (Pure rotation)
- Rotation about an axis of rotation (Combined translational and rotational motion)
- Rotation about an axis in the rotation (rotating axis)