A thin convex lens is made of two materials with refractive indices $n_1$ and $n_2$, as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. / is the focal length of the lens when $n_1$ = $n_2$ = n. The focal length is $f+\Delta f$ when $n_1$ = n and $n_2 = n + \Delta n$. Assuming $\Delta n << (n ? 1)$ and $1 < n < 2$, the correct statement(s) is/are,
- $\left|\frac{\Delta f}{f}\right|
- For $n = 1.5, \Delta n = 10^{-3}$ and $f = 20$ cm, the value of $\left|\Delta f\right|$ will be 0.02 cm (round off to $2^{nd}$ decimal place)
- If $\frac{\Delta n}{n}<0$ then $\frac{\Delta f}{f}>0$
- The relation between $ \frac{\Delta f}{f}$ and $\frac{\Delta n}{n}$ remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature
The Correct Option is D
Solution and Explanation
$\frac{1}{f}=\frac{\left(n_{1}-1\right)}{R}+\frac{n_{2}-1}{R}=\frac{\left(n_{1}+n_{2}-2\right)}{R}$
Now $\frac{\Delta f}{f^{2}}=\frac{\Delta n}{R}$
$\frac{\Delta f}{f}=\frac{\Delta n}{\left(n_{1}+n_{2}-2\right)}=\frac{\Delta n}{\left[2n+\Delta n-2\right]}$
For $n_{1}=n_{2}=1.5\quad\Delta n=10^{-3}, f=20cm then R = 20 cm$
and $\Delta f=\frac{10^{-3}\times20}{\left(2\times1.5-2+10^{-3}\right)}=0.02\,cm.$
If $\frac{\Delta n}{n}<0\left(Diversing nature increases\right) \,\therefore\frac{\Delta f}{f}>0$
If the surfaces are replaced by concave surfaces of same radius, focal length changes the sign withsame magnitude.
$\therefore\frac{\Delta f}{f}=\frac{\Delta n}{\left(2n+\Delta n-2\right)}$ (remain unchanged).
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in JEE Advanced exam
The reaction sequence given below is carried out with 16 moles of X. The yield of the major product in each step is given below the product in parentheses. The amount (in grams) of S produced is ____.

Use: Atomic mass (in amu): H = 1, C = 12, O = 16, Br = 80- JEE Advanced - 2025
- Organic Chemistry
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):

- JEE Advanced - 2025
- Waves and Oscillations
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
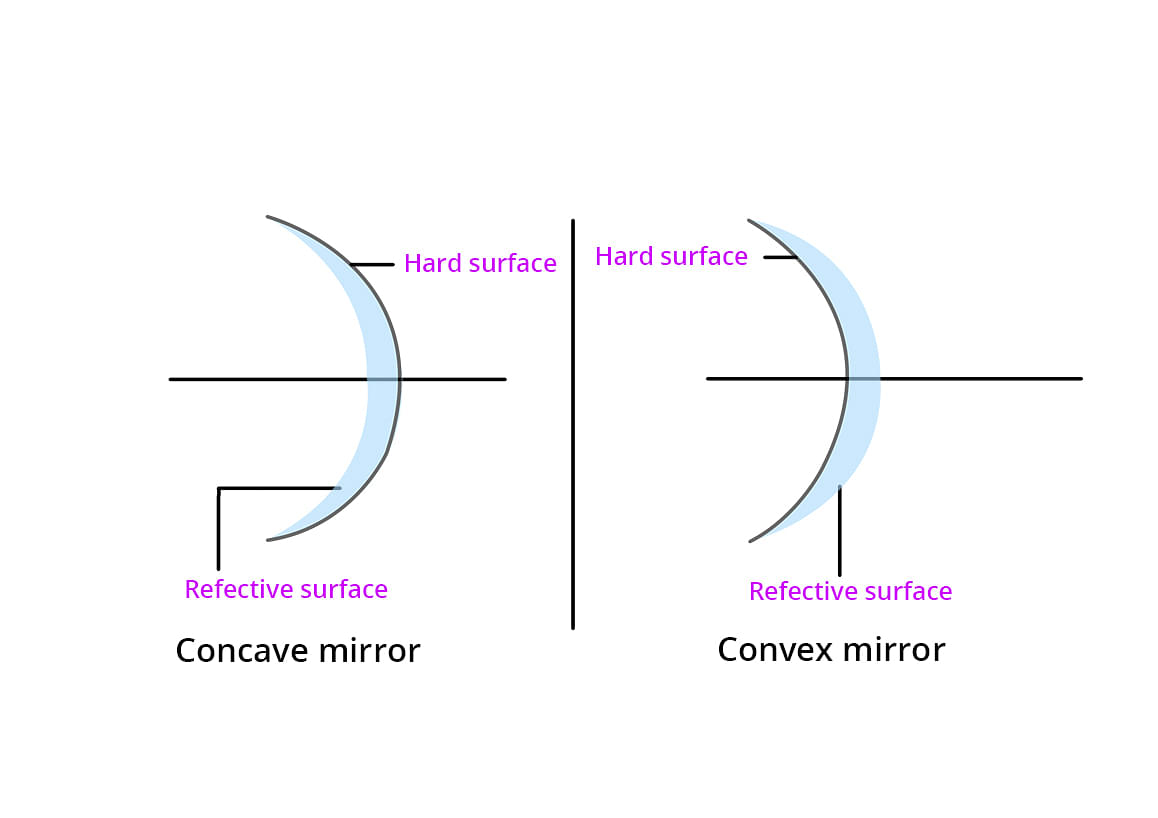
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.