Question:
A source of sound $S$ emitting waves of frequency $100\, Hz$ and an observor $O$ are located at some distance from each other. The source is moving with a speed of $19.4\, m s^{-1}$ at an angle of $60^{\circ}$ with the source observer line as shown in the figure. The observor is at rest. The apparent frequency observed by the observer is (velocity of sound in air $330\, ms ^{-1}$ )
A source of sound $S$ emitting waves of frequency $100\, Hz$ and an observor $O$ are located at some distance from each other. The source is moving with a speed of $19.4\, m s^{-1}$ at an angle of $60^{\circ}$ with the source observer line as shown in the figure. The observor is at rest. The apparent frequency observed by the observer is (velocity of sound in air $330\, ms ^{-1}$ )
Updated On: Dec 17, 2025
- 103 Hz
- 106 Hz
- 97 Hz
- 100 Hz
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Here, original frequency of sound, $f_{0}=100 \,Hz$
Speed of source $V_{s} 19.4 \cos 60^{\circ}=9.7$
From Doppler's formula
$f^{1}=f_{0}\left(\frac{V-V_0}{V-V_{s}}\right)$
$f^{1}=100\left(\frac{V-0}{V-(+9.7)}\right)$
$f^{1} 100 \frac{V}{V\left(1-\frac{9.7}{V}\right)}$ $f^{1}=100\left(1+\frac{9.7}{330}\right)=103 \,Hz$
Apparent frequency $f^{1}=103 \,Hz$
Was this answer helpful?
1
0
Top Questions on doppler effect
- When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
- AP EAPCET - 2025
- Physics
- doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
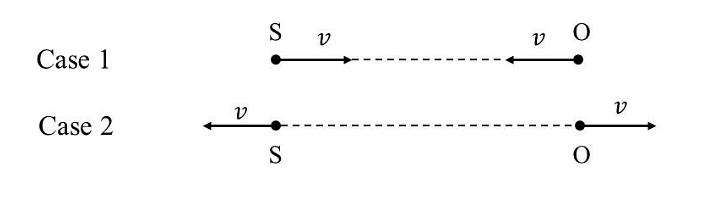
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
View More Questions
Questions Asked in BITSAT exam
- A simple pendulum has a time period of 2 s on Earth's surface. What is its time period at a height equal to the Earth's radius (R)? (Acceleration due to gravity at height h is \( g_h = \frac{g}{(1 + h/R)^2} \)).
- BITSAT - 2025
- Mechanics
- What is the dot product of the vectors \( \mathbf{a} = (2, 3, 1) \) and \( \mathbf{b} = (1, -1, 4) \)?
- BITSAT - 2025
- Vector Algebra
For the reaction \( A + B \to C \), the rate law is found to be \( \text{rate} = k[A]^2[B] \). If the concentration of \( A \) is doubled and \( B \) is halved, by what factor does the rate change?
- BITSAT - 2025
- Chemical Kinetics
- A coil of resistance 10 \( \Omega \) is connected to a battery of 12 V. If the current flowing through the coil is 2 A, what is the power dissipated in the coil?
- BITSAT - 2025
- Resistance
- A particle moves along the x-axis under a force $ F(x) = 6x^2 $ N. The work done by this force in moving the particle from $ x = 1 \, \text{m} $ to $ x = 2 \, \text{m} $ is:
- BITSAT - 2025
- work, energy and power
View More Questions
Concepts Used:
Doppler Effect
The Doppler effect is a phenomenon caused by a moving wave source that causes an apparent upward shift in frequency for observers who are approaching the source and a visible downward change in frequency for observers who are retreating from the source. It's crucial to note that the impact isn't caused by a change in the source's frequency.

The Doppler effect may be seen in any wave type, including water waves, sound waves, and light waves. We are most familiar with the Doppler effect because of our encounters with sound waves