Question:
A solid copper cube of $7 \,cm$ edge is subjected to a hydraulic pressure of $8000\, kPa$. The volume contraction of the copper cube is (Bulk modulus of copper = $140 \,GPa$ )
A solid copper cube of $7 \,cm$ edge is subjected to a hydraulic pressure of $8000\, kPa$. The volume contraction of the copper cube is (Bulk modulus of copper = $140 \,GPa$ )
Updated On: Apr 4, 2024
- $ 196 \times 10^{-3} cm^3$
- $ 19.6 \times 10^{-6} cm^3$
- $ 19.6 \times 10^{-3} cm^3$
- $ 196 \times 10^{3} cm^3$
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Given,
edge of solid copper cube, $l=7 \,cm$
hydraulic pressure, $p=8000 \,kPa =8000 \times 10^{3}\, Pa$
and Bulk modulus of copper, $\beta=140\, GPa$
$=140 \times 10^{9} \,Pa$
As we know that,
Bulk modulus, $\beta=\frac{p}{\left(\frac{\Delta V}{V}\right)}$
or $\beta=\frac{p V}{\Delta V}$
$\therefore \Delta V=\frac{p V}{\beta} =\frac{8000 \times 10^{3} \times(l)^{3}}{140 \times 10^{9}} $
$=\frac{8000 \times 10^{3} \times(7)^{3}}{140 \times 10^{9}}$
$=19.6 \times 10^{-3} \,cm ^{3} $
edge of solid copper cube, $l=7 \,cm$
hydraulic pressure, $p=8000 \,kPa =8000 \times 10^{3}\, Pa$
and Bulk modulus of copper, $\beta=140\, GPa$
$=140 \times 10^{9} \,Pa$
As we know that,
Bulk modulus, $\beta=\frac{p}{\left(\frac{\Delta V}{V}\right)}$
or $\beta=\frac{p V}{\Delta V}$
$\therefore \Delta V=\frac{p V}{\beta} =\frac{8000 \times 10^{3} \times(l)^{3}}{140 \times 10^{9}} $
$=\frac{8000 \times 10^{3} \times(7)^{3}}{140 \times 10^{9}}$
$=19.6 \times 10^{-3} \,cm ^{3} $
Was this answer helpful?
18
0
Top Questions on elastic moduli
- The slope of the stress-strain curve in the elastic deformation region is
- JKCET - 2024
- Physics
- elastic moduli
- The law which states that within elastic limits strain produced is proportional to the stress producing it is known as
- JKCET - 2024
- Physics
- elastic moduli
- A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5 cm. Another wire of the same material of length 4L and radius 4r is pulled by a force 4F under same conditions. The increase in length of this wire is ___ cm.
- JEE Main - 2022
- Physics
- elastic moduli
The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
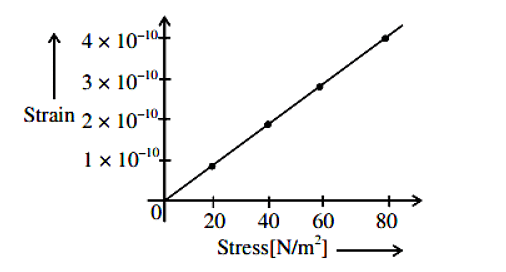
- JEE Main - 2022
- Physics
- elastic moduli
- If the length of a wire is made double and radius is halved of its respective values. Then, the Young’s modulus of the material of the wire will :
- JEE Main - 2022
- Physics
- elastic moduli
View More Questions
Questions Asked in AP EAPCET exam
- In a series LCR circuit, the voltages across the capacitor, resistor, and inductor are in the ratio 2:3:6. If the voltage of the source in the circuit is 240 V, then the voltage across the inductor is
- AP EAPCET - 2025
- Electromagnetic induction
- 0.25 moles of $ \text{CH}_2\text{FCOOH} $ was dissolved in $ 0.5 \, \text{kg} $ of water. The depression in freezing point of the resultant solution was observed as $ 1^\circ \text{C} $. What is the van't Hoff factor? ($ K_f = 1.86 \, \text{K kg mol}^{-1} $)
- AP EAPCET - 2025
- Colligative Properties
- At $T(K)$, the vapor pressure of water is $x$ kPa. What is the vapor pressure (in kPa) of 1 molal solution containing non-volatile solute?
- AP EAPCET - 2025
- Colligative Properties
- At 300 K, vapour pressure of pure liquid A is 70 mm Hg. It forms an ideal solution with liquid B. Mole fraction of B = 0.2 and total vapour pressure of solution = 84 mm Hg. What is vapour pressure (in mm) of pure B?
- AP EAPCET - 2025
- Colligative Properties
- A 1% (w/v) aqueous solution of a certain solute is isotonic with a 3% (w/v) solution of glucose (molar mass 180 g mol$^{-1}$). The molar mass of solute (in g mol$^{-1}$) is
- AP EAPCET - 2025
- Colligative Properties
View More Questions