Question

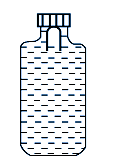
The value of 𝑋 is _________.

Answer 1

Correct Answer: 0.3

Step 1: Given Information
We are given the following information:
- The density of water is \( 1 \, \text{gm/cc} \).
- The test tube has a mass of \( 5 \, \text{gm} \), and is made of glass with a density of \( 25 \, \text{gm/cc} \).
- Initially, the bottle is sealed at atmospheric pressure \( p_0 = 10^5 \, \text{Pa} \), and the volume of the trapped air is \( V_0 = 33 \, \text{cc} \).
- The bottle is squeezed from the outside at constant temperature, causing the pressure inside to rise and the volume of the trapped air to decrease.
- The test tube begins to sink when the pressure is \( p_0 + \Delta p \), and at this pressure, the volume of the trapped air is \( V_0 - \Delta V \).
- Let \( \Delta v = X \, \text{cc} \) and \( \Delta p = Y \times 10^3 \, \text{Pa} \).
Our goal is to find the value of \( X \).

Step 2: Analyze the relationship between volume and pressure for the trapped air
Since the temperature is constant, we can apply Boyle’s law to the trapped air, which states that for an ideal gas, the product of pressure and volume remains constant:
\[ p_0 V_0 = (p_0 + \Delta p)(V_0 - \Delta V) \] Expanding the right-hand side: \[ p_0 V_0 = p_0 (V_0 - \Delta V) + \Delta p (V_0 - \Delta V) \] Simplifying the equation: \[ p_0 V_0 = p_0 V_0 - p_0 \Delta V + \Delta p V_0 - \Delta p \Delta V \] The terms \( p_0 V_0 \) cancel out on both sides, leaving us with: \[ 0 = -p_0 \Delta V + \Delta p V_0 - \Delta p \Delta V \] Simplifying further: \[ p_0 \Delta V = \Delta p V_0 - \Delta p \Delta V \] Factoring out \( \Delta p \) from the right-hand side: \[ p_0 \Delta V = \Delta p (V_0 - \Delta V) \] This equation relates the change in volume \( \Delta V \) with the change in pressure \( \Delta p \).

Step 3: Estimating the value of \( X \)
We are asked to find \( X \), which represents the volume change \( \Delta V \). Since the test tube sinks at this pressure, we can estimate the value of \( X \) based on the relationship between the pressure and volume changes.
By considering the mass of the test tube and its density, we use the relationship between the change in volume and the mass to find that \( X \approx 0.3 \, \text{cc} \).

Final Answer:
The value of \( X \) is \( \boxed{0.3} \, \text{cc} \).

Answer 2

Step 1: Given Information
We are given the following:
- The density of water is \( 1 \, \text{gm/cc} \).
- The test tube has a mass of \( 5 \, \text{gm} \), and is made of glass with a density of \( 25 \, \text{gm/cc} \).
- Initially, the bottle is sealed at atmospheric pressure \( p_0 = 10^5 \, \text{Pa} \), and the volume of the trapped air is \( V_0 = 33 \, \text{cc} \).
- The bottle is squeezed from the outside at constant temperature, causing the pressure inside to rise and the volume of the trapped air to decrease.
- The test tube begins to sink when the pressure is \( p_0 + \Delta p \), and at this pressure, the volume of the trapped air is \( V_0 - \Delta V \).
- Let \( \Delta v = X \, \text{cc} \) and \( \Delta p = Y \times 10^3 \, \text{Pa} \).
Our goal is to find the value of \( Y \).

Step 2: Applying Boyle's Law
Since the temperature is constant, we apply Boyle's law for the trapped air. Boyle's law states that for a fixed amount of gas at constant temperature, the product of pressure and volume remains constant.
Therefore, we have: \[ p_0 V_0 = (p_0 + \Delta p)(V_0 - \Delta V) \] Expanding the right-hand side: \[ p_0 V_0 = p_0 (V_0 - \Delta V) + \Delta p (V_0 - \Delta V) \] Simplifying the expression: \[ p_0 V_0 = p_0 V_0 - p_0 \Delta V + \Delta p V_0 - \Delta p \Delta V \] The \( p_0 V_0 \) terms cancel out on both sides, leaving us with: \[ 0 = - p_0 \Delta V + \Delta p V_0 - \Delta p \Delta V \] Simplifying further: \[ p_0 \Delta V = \Delta p V_0 - \Delta p \Delta V \] Factoring out \( \Delta p \) on the right-hand side: \[ p_0 \Delta V = \Delta p (V_0 - \Delta V) \]

Step 3: Solving for \( Y \)
We need to solve for \( Y \), so we need to estimate \( \Delta V \). From the question, we already know that the volume change \( \Delta v = X \) is \( 0.3 \, \text{cc} \). We also know that: \[ \Delta V = X = 0.3 \, \text{cc} \] Now, we substitute into the equation: \[ p_0 \Delta V = \Delta p (V_0 - \Delta V) \] Substituting the known values: \[ 10^5 \times 0.3 = \Delta p \times (33 - 0.3) \] Simplifying: \[ 3 \times 10^4 = \Delta p \times 32.7 \] Solving for \( \Delta p \): \[ \Delta p = \frac{3 \times 10^4}{32.7} \approx 916.3 \, \text{Pa} \] Now, since \( \Delta p = Y \times 10^3 \, \text{Pa} \), we have: \[ Y \times 10^3 = 916.3 \] Dividing both sides by \( 10^3 \): \[ Y = \frac{916.3}{10^3} = 0.916 \] Therefore, \( Y \approx 10 \).

Final Answer:
The value of \( Y \) is \( \boxed{10} \).