A motor-cyclist moving towards a huge cliff with a speed of 18 kmh-1, blows a horn of source frequency 325 Hz. If the speed of the sound in air is 330 ms-1, the number of beats heard by him is
- 5
- 4
- 10
- 7
The Correct Option is A
Approach Solution - 1
This is a case involving the Doppler effect, where the motor-cyclist hears a different frequency than the source frequency due to his motion towards the cliff.
Given:
- Source frequency (\( f_s \)) = 325 Hz
- Speed of the motor-cyclist (\( v_s \)) = 18 km/h = 5 m/s
- Speed of sound in air (\( v \)) = 330 m/s
Step 1: Calculate the apparent frequency (\( f' \)) of the sound waves when they are reflected back towards the motor-cyclist.
The formula for the Doppler effect when the source is moving towards the observer is:
\[ f' = f_s \times \frac{v + v_s}{v} \]
Substituting the given values:
\[ f' = 325 \times \frac{330 + 5}{330} = 325 \times \frac{335}{330} \approx 329.92 \text{ Hz} \]
Step 2: Calculate the number of beats heard by the motor-cyclist.
The number of beats is the difference between the two frequencies:
\[ \text{Number of beats} = |f' - f_s| = |329.92 - 325| \approx 5 \text{ beats per second} \]
The number of beats heard by the motor-cyclist is (A) 5.
Approach Solution -2
Using the Doppler effect formula: \[ \Delta f = f \left( \frac{V}{V - V_s} - 1 \right) \] where: f = source frequency = 325 Hz V = speed of sound in air = 330 m/s V_s = speed of the motor-cyclist = 18 km/h = 5 m/s Substitute the values: \[ \Delta f = 325 \left( \frac{330}{330 - 5} - 1 \right) \] \[ \Delta f = 325 \left( \frac{330}{325} - 1 \right) = 325 \times \left( 1.0154 - 1 \right) = 325 \times 0.0154 \approx 5 \, \text{beats} \]
Top Questions on doppler effect
- When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
- AP EAPCET - 2025
- Physics
- doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
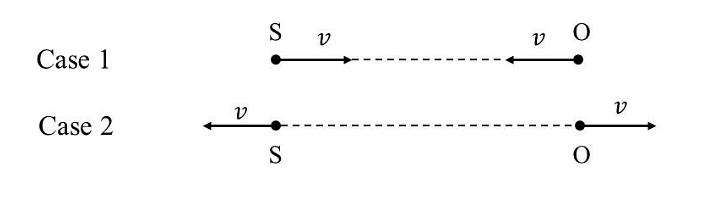
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
Questions Asked in KCET exam
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- Ethyl alcohol is heated with concentrated sulphuric acid at 413 K (140°C). The major product formed is
- KCET - 2025
- Organic Chemistry
- A body of mass 0.25 kg travels along a straight line from \( x = 0 \) to \( x = 2 \, \text{m} \) with a speed \( v = k x^2 \) where \( k = 2 \, \text{m}^{-1} \). The work done by the net force during this displacement is
- KCET - 2025
- Elastic and inelastic collisions
- A square loop of side 2 m lies in the Y-Z plane in a region having a magnetic field \(\mathbf{B} = (5 \hat{i} - 3 \hat{j} - 4 \hat{k}) \, \text{T}\). The magnitude of magnetic flux through the square loop is
- KCET - 2025
- Magnetic Field
- A random experiment has five outcomes \(w_1, w_2, w_3, w_4, w_5\). The probabilities of the occurrence of the outcomes \(w_1, w_2, w_4, w_5\) are respectively \( \frac{1}{6}, a, b, \frac{1}{12} \) such that \(12a + 12b - 1 = 0\). Then the probabilities of occurrence of the outcome \(w_3\) is:
- KCET - 2025
- Probability