A cylindrical tube, with its base as shown in the figure, is filled with water It is moving down with a constant acceleration $a$ along a fixed inclined plane with angle $\theta=45^{\circ} P_{1}$ and $P_{2}$ are pressures at points $1$ and $2$, respectively located at the base of the tube Let $\beta=\left(P_{1}-P_{2}\right) /(\rho g d)$, where $\rho$ is density of water, $d$ is the inner diameter of the tube and $g$ is the acceleration due to gravity Which of the following statement(s) is(are) correct?
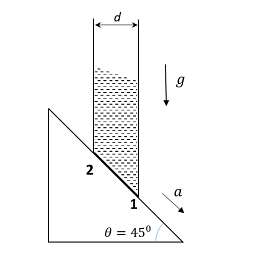
A cylindrical tube, with its base as shown in the figure, is filled with water It is moving down with a constant acceleration $a$ along a fixed inclined plane with angle $\theta=45^{\circ} P_{1}$ and $P_{2}$ are pressures at points $1$ and $2$, respectively located at the base of the tube Let $\beta=\left(P_{1}-P_{2}\right) /(\rho g d)$, where $\rho$ is density of water, $d$ is the inner diameter of the tube and $g$ is the acceleration due to gravity Which of the following statement(s) is(are) correct?
$\beta=0$ when $a=\frac {g}{\sqrt{2}}$
$\beta > 0$ when $a=\frac{g}{\sqrt{2}}$
$\beta=\frac{\sqrt{2}-1}{\sqrt{2}}$ when $a =\frac{g}{2}$
$\beta=\frac{1}{\sqrt{2}}$ when $a = \frac{g}{2}$
The Correct Option is C
Solution and Explanation
The correct answer is option (C): $\beta=\frac{\sqrt{2}-1}{\sqrt{2}}$ when $a =\frac{g}{2}$
Top Questions on mechanical properties of fluid
- The magnifying power of a telescope is \( 9 \). When adjusted for parallel rays, the distance between the objective and eyepiece is 20 cm. The ratio of the focal length of the objective lens to the focal length of the eyepiece is:
- BITSAT - 2024
- Physics
- mechanical properties of fluid
- A hole of area 1 mm\(^2\) opens in the pipe near the lower end of a large water storage tank, and a stream of water shoots from it. If the top of the water in the tank is 20 m above the point of the leak, the amount of water escapes in 1 s is:
- OJEE - 2024
- Physics
- mechanical properties of fluid
- The volume of an air bubble is doubled as it rises from the bottom of a lake to its surface. The atmospheric pressure is 75 cm of mercury and the ratio of the density of mercury to that of lake water is 40/3. The depth of the lake is:
- OJEE - 2024
- Physics
- mechanical properties of fluid
- Water is flowing through a tube of radius \( r \) with a speed \( v \). If this tube is joined to another tube of radius \( r/2 \), the speed of water in the second tube is:
- OJEE - 2024
- Physics
- mechanical properties of fluid
- The increase in pressure required to decrease the volume of 200 L of water by 0.004 percent is (Bulk modulus of water is \( 2.1 \times 10^9 \) N/m\(^2\)):
- OJEE - 2024
- Physics
- mechanical properties of fluid
Questions Asked in JEE Advanced exam
- Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
- JEE Advanced - 2024
- Matrices
- A positive, singly ionized atom of mass number \( A_M \) is accelerated from rest by the voltage \( 192 \, \text{V} \). Thereafter, it enters a rectangular region of width \( w \) with magnetic field \( \vec{B}_0 = 0.1\hat{k} \, \text{T} \). The ion finally hits a detector at the distance \( x \) below its starting trajectory. Which of the following option(s) is(are) correct? \[ \text{(Given: Mass of neutron/proton = } \frac{5}{3} \times 10^{-27} \, \text{kg, charge of the electron = } 1.6 \times 10^{-19} \, \text{C).} \]
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass \( m \) and radius \( r \) and is in a uniform vertical magnetic field \( B_0 \). When a current \( I \) is passed through the loop, the loop turns about the line PQ by an angle \( \theta \). The angle \( \theta \) is given by:
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A region in the form of an equilateral triangle (in x-y plane) of height \( L \) has a uniform magnetic field \( \mathbf{B} \) pointing in the \( +z \)-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height \( L \), is placed in the x-y plane with its vertex \( P \) at \( x = 0 \) in the orientation shown in the figure. At \( t = 0 \), the loop starts entering the region of the magnetic field with a uniform velocity \( \mathbf{v} \) along the \( +x \)-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
Which of the following graphs best depicts the variation of the induced emf (\( \mathcal{E} \)) in the loop as a function of the distance (\( x \)) starting from \( x = 0 \)?- JEE Advanced - 2024
- Radioactivity
- A table tennis ball has radius \( \frac{3}{2} \times 10^{-2} \, \text{m} \) and mass \( \frac{22}{7} \times 10^{-3} \, \text{kg} \). It is slowly pushed down into a swimming pool to a depth \( d = 0.7 \, \text{m} \) below the water surface and then released from rest. It emerges from the water surface at speed \( v \), without getting wet, and rises to a height \( H \). Which of the following option(s) is(are) correct?\(\text{(Given: } \pi = \frac{22}{7}, g = 10 \, \text{m/s}^2, \text{density of water} = 1 \times 10^3 \, \text{kg/m}^3, \text{viscosity of water} = 1 \times 10^{-3} \, \text{Pa.s).}\)
- JEE Advanced - 2024
- Radioactivity
Concepts Used:
Mechanical Properties of Fluid
The science of the mechanical properties of fluids is called Hydrostatics. A fluid is a substance that relents to the slightest pressure. Fluids are categorized into two classes famed by the names of liquids, and elastic fluids or gases, which later comprehend the air of the atmosphere and all the different kinds of air with which chemistry makes us acquainted.
Streamline Flow:
A streamline is a curve the tangent to which at any point provides the direction of the fluid velocity at that point. It is comparable to a line of force in an electric or magnetic field. In steady flow, the pattern of the streamline is motionless or static with time, and therefore, a streamline provides the actual path of a fluid particle.
Tube of Flow:
A tubular region of fluid enclosed by a boundary comprises streamlines is called a tube of flow. Fluid can never cross the boundaries of a tube of flow and therefore, a tube of flow acts as a pipe of the same shape.
Surface Tension and Viscosity:
The surface tension of a liquid is all the time a function of the solid or fluid with which the liquid is in contact. If a value for surface tension is provided in a table for oil, water, mercury, or whatever, and the contacting fluid is unspecified, it is safe to consider that the contacting fluid is air.