Question:
A convex lens of glass is immersed in water compared to its power in air, its power in water will
A convex lens of glass is immersed in water compared to its power in air, its power in water will
Updated On: Sep 3, 2024
- increase
- decrease
- not change
- decrease for red light increase for violet light
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The correct option is: (B): decrease.
When a convex lens is immersed in water, its focal length increases, resulting in a decrease in its power.
According to the lens maker's formula:
\(\frac{1}{f}=(\frac{μ_2}{μ_1}−1)(\frac{1}{R_1}-\frac{1}{R_2})\)
When the lens is immersed in water, the refractive index of the medium μ1 increases from 1 to \(\frac{4}{3}\) (the refractive index of water). As a result, the \(\frac{μ_2}{μ_1}\) term decreases, causing the \((\frac{μ_2}{μ_1}-1)\) term to decrease, which leads to a decrease in \(\frac{1}{f}\) Therefore, the power \((=\frac{1}{f})\) decreases.
When a convex lens is immersed in water, its focal length increases, resulting in a decrease in its power.
According to the lens maker's formula:
\(\frac{1}{f}=(\frac{μ_2}{μ_1}−1)(\frac{1}{R_1}-\frac{1}{R_2})\)
When the lens is immersed in water, the refractive index of the medium μ1 increases from 1 to \(\frac{4}{3}\) (the refractive index of water). As a result, the \(\frac{μ_2}{μ_1}\) term decreases, causing the \((\frac{μ_2}{μ_1}-1)\) term to decrease, which leads to a decrease in \(\frac{1}{f}\) Therefore, the power \((=\frac{1}{f})\) decreases.
Was this answer helpful?
7
11
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
View More Questions
Questions Asked in CBSE CLASS XII exam
- The principal value of \( \cot^{-1} \left( -\frac{1}{\sqrt{3}} \right) \) is:
- CBSE CLASS XII - 2025
- Inverse Trigonometric Functions
- Why does M. Hamel refer to language as a key to freedom from slavery? (The Last Lesson)
- CBSE CLASS XII - 2025
- The Last Lesson
- Bama and Zitkala-Sa have proven that education is the antidote to all social evils. Analyse their characters in terms of their struggles and their will to win. (Memories of Childhood)
- CBSE CLASS XII - 2025
- Literature
“One of these days you’re going to talk yourself into a load of trouble,” her father said aggressively. What do you learn about Sophie’s father from these lines? (Going Places)
- CBSE CLASS XII - 2025
- Literature
- Explain the transmission of optical signal through an optical fiber with a diagram.
- CBSE CLASS XII - 2025
- Ray optics and optical instruments
View More Questions
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
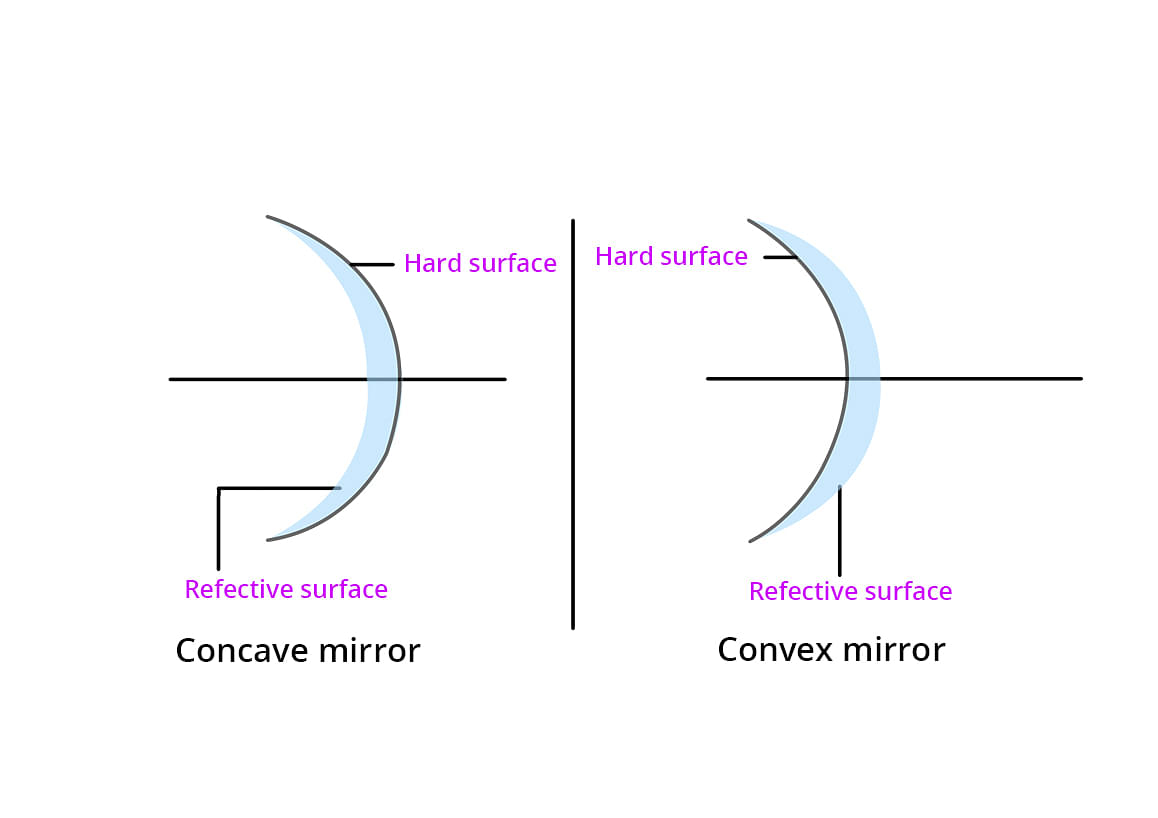
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.