Question:
Two point charges $- Q$ and $+ Q / \sqrt{3}$ are placed in the $xy$-plane at the origin $(0,0)$ and a point $(2,0)$, respectively, as shown in the figure This results in an equipotential circle of radius $R$ and potential $V=0$ in the $x y$-plane with its center at $(b, 0)$ All lengths are measured in meters The value of $R$ is _______ meter
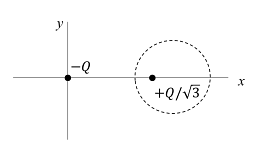
Two point charges $- Q$ and $+ Q / \sqrt{3}$ are placed in the $xy$-plane at the origin $(0,0)$ and a point $(2,0)$, respectively, as shown in the figure This results in an equipotential circle of radius $R$ and potential $V=0$ in the $x y$-plane with its center at $(b, 0)$ All lengths are measured in meters The value of $R$ is _______ meter
Updated On: May 22, 2024
Hide Solution
Verified By Collegedunia
Correct Answer: 1.73
Solution and Explanation
Answer: 1.73
Was this answer helpful?
0
0
Top Questions on Electrostatic potential
- The electrostatic potential energy of the electron in an orbit of hydrogen is \( -6.8 \) eV. The speed of the electron in this orbit is (C is the speed of light in vacuum):
- AP EAMCET - 2024
- Physics
- Electrostatic potential
- When a parallel plate capacitor is charged up to 95 V, its capacitance is \( C \). If a dielectric slab of thickness 2 mm is inserted between plates and the plate separation is increased by 1.6 mm such that the potential difference remains constant, find the dielectric constant of the material:
- AP EAMCET - 2024
- Physics
- Electrostatic potential
- Electric field intensity and electric potential at a point due to a point charge are 600 V/m and -3600 V respectively. The distance of the point from the charge and the magnitude of the charge are:
- AP EAMCET - 2024
- Physics
- Electrostatic potential
- βIntroduction of a small charged sphere into a larger one allows us to keep piling up a larger and larger amount of charge on the latterβ β This is the principle of the:
- AP EAMCET - 2024
- Physics
- Electrostatic potential
- Two separated conducting spheres \(S_1\) and \(S_2\), of radii \(3R/4\) and \(R/4\) having \(15 \mu C\) and \(-3 \mu C\) charges respectively are at a large distance. They are now connected by a conducting wire. After a long time, the charges on \(S_1\) and \(S_2\) respectively are:
- AP EAMCET - 2024
- Physics
- Electrostatic potential
View More Questions
Questions Asked in JEE Advanced exam
- Let \(S=\left\{\begin{pmatrix} 0 & 1 & c \\ 1 & a & d\\ 1 & b & e \end{pmatrix}:a,b,c,d,e\in\left\{0,1\right\}\ \text{and} |A|\in \left\{-1,1\right\}\right\}\), where |A| denotes the determinant of A. Then the number of elements in S is _______.
- JEE Advanced - 2024
- Matrices
- A positive, singly ionized atom of mass number \( A_M \) is accelerated from rest by the voltage \( 192 \, \text{V} \). Thereafter, it enters a rectangular region of width \( w \) with magnetic field \( \vec{B}_0 = 0.1\hat{k} \, \text{T} \). The ion finally hits a detector at the distance \( x \) below its starting trajectory. Which of the following option(s) is(are) correct? \[ \text{(Given: Mass of neutron/proton = } \frac{5}{3} \times 10^{-27} \, \text{kg, charge of the electron = } 1.6 \times 10^{-19} \, \text{C).} \]
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass \( m \) and radius \( r \) and is in a uniform vertical magnetic field \( B_0 \). When a current \( I \) is passed through the loop, the loop turns about the line PQ by an angle \( \theta \). The angle \( \theta \) is given by:
- JEE Advanced - 2024
- Electromagnetic Field (EMF)
- A region in the form of an equilateral triangle (in x-y plane) of height \( L \) has a uniform magnetic field \( \mathbf{B} \) pointing in the \( +z \)-direction. A conducting loop PQR, in the form of an equilateral triangle of the same height \( L \), is placed in the x-y plane with its vertex \( P \) at \( x = 0 \) in the orientation shown in the figure. At \( t = 0 \), the loop starts entering the region of the magnetic field with a uniform velocity \( \mathbf{v} \) along the \( +x \)-direction. The plane of the loop and its orientation remain unchanged throughout its motion.
Which of the following graphs best depicts the variation of the induced emf (\( \mathcal{E} \)) in the loop as a function of the distance (\( x \)) starting from \( x = 0 \)?- JEE Advanced - 2024
- Radioactivity
- A table tennis ball has radius \( \frac{3}{2} \times 10^{-2} \, \text{m} \) and mass \( \frac{22}{7} \times 10^{-3} \, \text{kg} \). It is slowly pushed down into a swimming pool to a depth \( d = 0.7 \, \text{m} \) below the water surface and then released from rest. It emerges from the water surface at speed \( v \), without getting wet, and rises to a height \( H \). Which of the following option(s) is(are) correct?\(\text{(Given: } \pi = \frac{22}{7}, g = 10 \, \text{m/s}^2, \text{density of water} = 1 \times 10^3 \, \text{kg/m}^3, \text{viscosity of water} = 1 \times 10^{-3} \, \text{Pa.s).}\)
- JEE Advanced - 2024
- Radioactivity
View More Questions
Concepts Used:
Electrostatic Potential
The electrostatic potential is also known as the electric field potential, electric potential, or potential drop is defined as βThe amount of work that is done in order to move a unit charge from a reference point to a specific point inside the field without producing an acceleration.β
SI Unit of Electrostatic Potential:
SI unit of electrostatic potential - volt
Other units - statvolt
Symbol of electrostatic potential - V or Ο
Dimensional formula - ML2T3I-1
Electric Potential Formula:
The electric potential energy of the system is given by the following formula:
U = 1/(4ΟΡº) Γ [q1q2/d]
Where q1 and q2 are the two charges that are separated by the distance d.