There is a pentagonal shaped park as shown in the figure.

For finding its area Jyoti and Kavita divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area?

For finding its area Jyoti and Kavita divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area?
Solution and Explanation
(i) Jyoti’s way of finding the area is as follows:
Area of pentagon ABCDE = Area of trapezium ABCF + Area of trapezium AEDF
\(= \frac{1}{2} × (AF + BC) × FC + \frac{1}{2} × (AF + ED) × DF\)
\(= \frac{1}{2} × (30 m + 15 m) × \frac{15}{2} m + \frac{1}{2} × (30 + 15 m) × \frac{15}{2} m\)
\(= 2 × \frac{1}{2} (30 m + 15 m) × \frac{15}{2}\)
\(= 45 m × 7.5 m\)
\(= 337.5 m²\)
Thus, the area of the pentagonal shaped park according to Jyoti’s way is 337.5 m²
(ii) Kavitha’s way of finding the area is as follows:
Area of pentagon ABCDE = Area of triangle ABE + Area of square EBCD
\(= \frac{1}{2} × BE × (AF − OF) + FC × BC \) [Since, AO = AF - OF]
\(= \frac{1}{2} × 15 × (30 − 15) + (15 × 15 )\)
\(= (\frac{1}{2} × 15 × 15) m² + 225 m²\)
\(= 112.5 m² + 225 m²\)
\(= 337.5 m²\)
Thus, the area of the pentagonal shaped park according to Kavitha’s way is 337.5 m²
Top Questions on Area of a Polygon
- The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs 4.
- CBSE Class VIII
- Mathematics
- Area of a Polygon
- Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
- CBSE Class VIII
- Mathematics
- Area of a Polygon
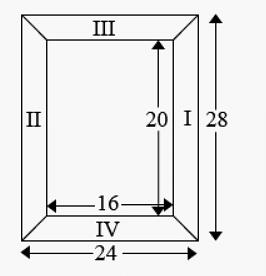
- Diagram of the adjacent picture frame has outer dimensions = 24 cm x 28 cm and inner dimensions 16 cm x 20 cm. Find the area of each section of the frame, if the width of each section is same.
- CBSE Class VIII
- Mathematics
- Area of a Polygon
- Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

- CBSE Class VIII
- Mathematics
- Area of a Polygon
- The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

- CBSE Class VIII
- Mathematics
- Area of a Polygon
Questions Asked in CBSE Class VIII exam
- Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
- CBSE Class VIII
- Addition and Subtraction of Algebraic Expressions
- Suppose 2 kg of sugar contains 9 x 106 crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
- CBSE Class VIII
- Direct Proportion
- Who had written the letter, to whom, and when?
- CBSE Class VIII
- The Best Christmas Present in the world
- Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
- CBSE Class VIII
- Addition and Subtraction of Algebraic Expressions
- Can the process of rusting be called combustion? Discuss.
- CBSE Class VIII
- Types of Combustion