The statement
\((p⇒q)∨(p⇒r) \)
is NOT equivalent to
The statement
\((p⇒q)∨(p⇒r) \)
is NOT equivalent to
\((p∧(∼r))⇒q\)
\((∼q)⇒((∼r)∨p)\)
\(p⇒(q∨r)\)
\((p∧(∼q))⇒r\)
The Correct Option is B
Approach Solution - 1
Let's analyze the given logical statement and its options to find which option is NOT equivalent to the statement \((p \Rightarrow q) \lor (p \Rightarrow r)\).
First, we will recall some fundamental concepts:
- The implication \(p \Rightarrow q\) is equivalent to \((\sim p) \lor q\).
- The equivalent transformation of multiple logical expressions helps in determining their equivalence.
Now, let's transform the given statement:
\((p \Rightarrow q) \lor (p \Rightarrow r)\) is equivalent to \(((\sim p) \lor q) \lor ((\sim p) \lor r)\).
Using the distributive law:
\(((\sim p) \lor q) \lor ((\sim p) \lor r) = (\sim p) \lor (q \lor r)\)
This further simplifies to:
\(p \Rightarrow (q \lor r)\)
Now, let's compare each option with the simplified statement:
- \((p \land (\sim r)) \Rightarrow q\)
This statement implies that if both \(p\) and \(\sim r\) are true, then \(q\) must be true. It is not directly equivalent to the original statement. - \((\sim q) \Rightarrow ((\sim r) \lor p)\)
Transforming, \(\sim q \Rightarrow (\sim r \lor p)\) becomes \(q \lor (\sim r \lor p)\), which is not equivalent to the simplified form. - \(p \Rightarrow (q \lor r)\)
Already derived as the simplified version of the original statement. - \((p \land (\sim q)) \Rightarrow r\)
This implies that if both \(p\) and \(\sim q\) are true, then \(r\) must be true. It could be considered equivalent in specific cases but doesn't match the general form derived above.
From the above analysis, it is clear that the option \((\sim q) \Rightarrow ((\sim r) \lor p)\) does not match the equivalent transformation of the statement \((p \Rightarrow q) \lor (p \Rightarrow r)\).
Therefore, the correct answer is: \((\sim q) \Rightarrow ((\sim r) \lor p)\)
Approach Solution -2
\((A)(p∧(∼r))⇒q\)
\(∼(p∧∼r)∨q\)
\(≡(∼p∨r)∨q\)
\(≡∼p∨(r∨q)\)
\(≡p→(q∨r)\)
\(≡(p⇒q)∨(p⇒r)\)
\((C)p⇒(q∨r)\)
\(≡∼p∨(q∨r)\)
\(≡(∼p∨q)∨(∼p∨r)\)
\(≡(p→q)∨(p→r)\)
\((D)(p∧∼q)⇒r\)
\(≡p⇒(q∨r)\)
\(≡(p⇒q)∨(p⇒r)\)
So, the correct option is (B): \((∼q)⇒((∼r)∨p)\)
Top Questions on types of differential equations
- Let the system of equations \(x+2y+3z = 5\), \(2x+3y+z = 9\), \(4x+3y+λz = μ\) have an infinite number of solutions. Then \(λ + 2μ\) is equal to
- JEE Main - 2024
- Mathematics
- types of differential equations
- If \( m_1 \) and \( m_2 \) are the slopes of the direct common tangents drawn to the circles \[ x^2 + y^2 - 2x - 8y + 8 = 0 \quad \text{and} \quad x^2 + y^2 - 8x + 15 = 0 \] then \( m_1 + m_2 \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If \( (2,3) \) is the focus and \( x - y + 3 = 0 \) is the directrix of a parabola, then the equation of the tangent drawn at the vertex of the parabola is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If the focus of an ellipse is \((-1,-1)\), equation of its directrix corresponding to this focus is \(x + y + 1 = 0\) and its eccentricity is \(\frac{1}{\sqrt{2}}\), then the length of its major axis is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The equation of the common tangent to the parabola \(y^2 = 8x\) and the circle \(x^2 + y^2 = 2\) is \(ax + by + 2 = 0\). If \(-\frac{a}{b}>0\), then \(3a^2 + 2b + 1 =\)
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Questions Asked in JEE Main exam
- A 20 m long uniform copper wire held horizontally is allowed to fall under the gravity (g = 10 m/s²) through a uniform horizontal magnetic field of 0.5 Gauss perpendicular to the length of the wire. The induced EMF across the wire when it travels a vertical distance of 200 m is_______ mV.}
- JEE Main - 2026
- Thermodynamics
- If the end points of chord of parabola \(y^2 = 12x\) are \((x_1, y_1)\) and \((x_2, y_2)\) and it subtend \(90^\circ\) at the vertex of parabola then \((x_1x_2 - y_1y_2)\) equals :
- JEE Main - 2026
- Probability
- The sum of all possible values of \( n \in \mathbb{N} \), so that the coefficients of \(x, x^2\) and \(x^3\) in the expansion of \((1+x^2)^2(1+x)^n\) are in arithmetic progression is :
- JEE Main - 2026
- Integration
- In a microscope of tube length $10\,\text{cm}$ two convex lenses are arranged with focal lengths $2\,\text{cm}$ and $5\,\text{cm}$. Total magnification obtained with this system for normal adjustment is $(5)^k$. The value of $k$ is ___.
- JEE Main - 2026
- Optical Instruments
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
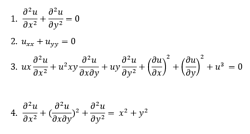
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
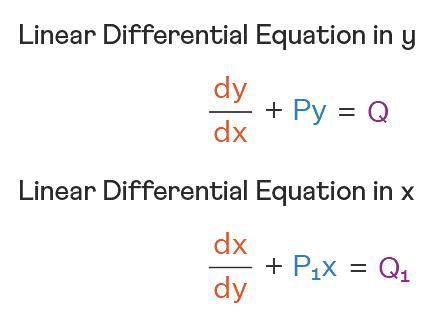
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations