The partial floral formula of a flower is $K_{\left(5\right)} C_{5}A_{\left(\infty\right)} \frac{G_{5}}{ }$ Which f the following set of information is conveyed here?
- Gamosepalous, polypetalous, syncarpous and superior ovary
- Polysepalous, polypetalous, syncarpous and inf rior ovary
- Gamosepalous, gamopetalous, polycarpou and superior ovary
- Gamosepalous, polypetalous, syncarpous and in erior ovary
The Correct Option is A
Solution and Explanation
Top Questions on The Inflorescence
- In a cymose type of inflorescence, the growth of the main axis terminates in a:
- UPSEE - 2016
- Biology
- The Inflorescence
- The inflorescence found in banana is
- UP CPMT - 2015
- Biology
- The Inflorescence
- The inflorescence in which sessile flowers are borne acropetally on an elongated rachis, it is called
- AMUEEE - 2014
- Biology
- The Inflorescence
- Which one of the following is correct explanation for the floral formula $\quad\quad\% \Theta K_{\left(5\right)} C_{1+2+\left(2\right)}A_{\left(9\right)+1 }G_{1}$
- KEAM - 2013
- Biology
- The Inflorescence
- Inflorescence of Liliaceae is
- AIIMS - 2011
- Biology
- The Inflorescence
Questions Asked in WBJEE exam
- ABC is an isosceles triangle with an inscribed circle with center O. Let P be the midpoint of BC. If AB=AC=15 and BC=10,then OP equals
- WBJEE - 2023
- Three Dimensional Geometry
- Let A=\(\begin{pmatrix} 0&0 &1 \\ 1&0 &0 \\ 0&0 &0 \end{pmatrix}\), B=\(\begin{pmatrix} 0&1 &0 \\ 0&0 &1 \\ 0&0 &0 \end{pmatrix}\) and P=\(\begin{pmatrix} 0&1 &0 \\ x&0 &0 \\ 0&0 &y \end{pmatrix}\) be an orthogonal matrix such that B=PAP-1 holds. Then
- WBJEE - 2023
- Matrices
Let α,β be the roots of the equation, ax2+bx+c=0.a,b,c are real and sn=αn+βn and \(\begin{vmatrix}3 &1+s_1 &1+s_2\\1+s_1&1+s_2 &1+s_3\\1+s_2&1+s_3 &1+s_4\end{vmatrix}=\frac{k(a+b+c)^2}{a^4}\) then k=
- WBJEE - 2023
- Complex Numbers and Quadratic Equations
- An electric dipole of dipole moment p is placed at the origin of the coordinate system along the z-axis. The amount of work required to move a charge 'q' from the point (a,0,0) to the point (0,0,a) is
- WBJEE - 2023
- Electric Dipole
- If \(\int \frac{dx}{(x+1)(x-2)(x-3)}=\frac{1}{k}log_e\left \{ \frac{|x-3|^3|x+1|}{(x-2)^4}\right \}+c\), then the value of k is
- WBJEE - 2023
- Integrals of Some Particular Functions
Concepts Used:
Inflorescence
The term inflorescence comes under the method morphology of flowering plants. The Morphology of flowering plants is the study of different parts of the plants, which includes the leaves, flowers, fruits, and stems. In a plant, the flowers either grow individually or in a set of groups, and the groups of flowers are referred to as inflorescence.
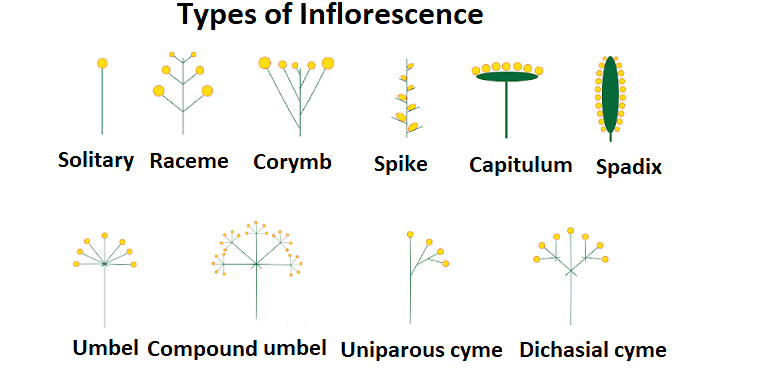
Inflorescence can also be referred to as the reproductive part of a plant that contains a group of flowers. It is responsible for the positioning of flowers on the floral axis and it is divided into two categories: racemose inflorescence and cymose inflorescence. In the racemose inflorescence, the main axis keeps on growing and the flower develops itself in an acropetal pattern while in the cymose inflorescence the termination of the main axis takes place and the flower grows in a basipetal pattern.