The orthocentre of the triangle formed by the lines $xy = 0$ and $ x+ y = 1$,is
- $\Bigg(\frac{1}{2}.\frac{1}{2}\Bigg)$
- $\Bigg(\frac{1}{3}.\frac{1}{3}\Bigg)$
- (0, 0)
- $\Bigg(\frac{1}{4}.\frac{1}{4}\Bigg)$
The Correct Option is C
Solution and Explanation
Top Questions on Straight lines
- The equation of a straight line is given by \( y = 3x + 4 \). What is the slope of the line?
- BITSAT - 2025
- Mathematics
- Straight lines
- Find the slope of the line passing through the points $ (1, 2) $ and $ (3, 6) $:
- BITSAT - 2025
- Mathematics
- Straight lines
- The equation of the line passing through the point \((1, 2)\) and perpendicular to the line \(3x + 4y - 12 = 0\) is:
- AP EAPCET - 2025
- Mathematics
- Straight lines
- Find the slope of the line perpendicular to the line $ 3x + 4y - 12 = 0 $.
- AP EAPCET - 2025
- Mathematics
- Straight lines
- Two straight lines \( 3x - 2y = 5 \) and \( 2x + ky + 7 = 0 \) are perpendicular to each other. The value of \( k \) is:
- JEECUP - 2024
- Mathematics
- Straight lines
Questions Asked in JEE Advanced exam
- One of the products formed from the reaction of permanganate ion with iodide ion in neutral aqueous medium is:
- JEE Advanced - 2025
- Redox reactions
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ S $ denote the locus of the point of intersection of the pair of lines $$ 4x - 3y = 12\alpha,\quad 4\alpha x + 3\alpha y = 12, $$ where $ \alpha $ varies over the set of non-zero real numbers. Let $ T $ be the tangent to $ S $ passing through the points $ (p, 0) $ and $ (0, q) $, $ q > 0 $, and parallel to the line $ 4x - \frac{3}{\sqrt{2}} y = 0 $.
Then the value of $ pq $ is- JEE Advanced - 2025
- Coordinate Geometry
- Let $ \mathbb{R} $ denote the set of all real numbers. Let $ a_i, b_i \in \mathbb{R} $ for $ i \in \{1, 2, 3\} $.
Define the functions $ f: \mathbb{R} \to \mathbb{R},\ g: \mathbb{R} \to \mathbb{R},\ h: \mathbb{R} \to \mathbb{R} $ by:
$$ f(x) = a_1 + 10x + a_2x^2 + a_3x^3 + x^4,\quad g(x) = b_1 + 3x + b_2x^2 + b_3x^3 + x^4, $$ $$ h(x) = f(x+1) - g(x+2) $$ If $ f(x) \ne g(x) $ for every $ x \in \mathbb{R} $, then the coefficient of $ x^3 $ in $ h(x) $ is:- JEE Advanced - 2025
- Polynomials
Let $ y(x) $ be the solution of the differential equation $$ x^2 \frac{dy}{dx} + xy = x^2 + y^2, \quad x > \frac{1}{e}, $$ satisfying $ y(1) = 0 $. Then the value of $ 2 \cdot \frac{(y(e))^2}{y(e^2)} $ is ________.
- JEE Advanced - 2025
- Differential equations
JEE Advanced Notification
GMC Azamgarh Admission 2025: Dates, Courses, Fees, Eligibility, SelectJuly 22, 2025Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:
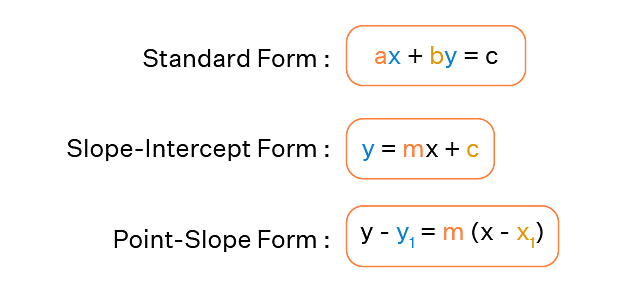
The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c