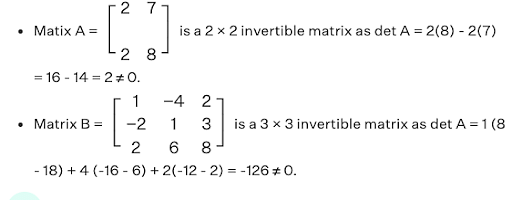Question:
The number of $3 \times 3$ non-singular matrices with four entries as $1$ and all other entries as $0$ is
The number of $3 \times 3$ non-singular matrices with four entries as $1$ and all other entries as $0$ is
Updated On: Aug 1, 2022
- 6
- at least 7
- less than 4
- 5
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The matrix $\begin{pmatrix}1&a&b\\ c&1&d\\ e&f&1\end{pmatrix}$
where exectly one of $a, b,c,d,e,f$ is 1 and rest of them are zero, is invertible. There are six such matrices.
Also the matrix $\begin{vmatrix}1&0&1\\ 0&1&0\\ 1&0&0\end{vmatrix}$ is invertible
Thus, there are at least 7 such matrices which are invertible.
Was this answer helpful?
0
0
Top Questions on Invertible Matrices
- If A is a non-identity invertible symmetric matrix, then \(A^{-1}\) is:
- CUET (UG) - 2023
- Mathematics
- Invertible Matrices
- The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- Which of the following matrices can NOT be obtained from the matrix \(\begin{bmatrix} -1 &2 \\ 1 & -1 \end{bmatrix}\) by a single elementary row operation?
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- If A and B are invertible matrices then which of the following is not correct ?
- KCET - 2021
- Mathematics
- Invertible Matrices
- The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
- KCET - 2019
- Mathematics
- Invertible Matrices
View More Questions
Questions Asked in AIEEE exam
- This question has Statement 1 and Statement 2. Of the four choices given after the Statements, choose the one that best describes the two Statements. It is not possible to make a sphere of capacity $1$ farad using a conducting material. It is possible for earth as its radius is $6.4 \times 10^6\,m$.
- AIEEE - 2012
- electrostatic potential and capacitance
- A steel wire can sustain $100\, kg$ weight without breaking. If the wire is cut into two equal parts, each part can sustain a weight of
- AIEEE - 2012
- mechanical properties of solids
- The limiting line in Balmer series will have a frequency of (Rydberg constant, $R_{\infty}=3.29\times10^{15}$ cycles/s)
- AIEEE - 2012
- Electromagnetic Spectrum
- Which of the plots shown in the figure represents speed (v) of the electron in a hydrogen atom as a function of the principal quantum number (n)?
- The ratio of number of oxygen atoms (O) in 16.0 g ozone $(O_3), \,28.0\, g$ carbon monoxide $(CO)$ and $16.0$ oxygen $(O_2)$ is (Atomic mass: $C = 12,0 = 16$ and Avogadro?? constant $N_A = 6.0 x 10^{23}\, mol^{-1}$)
- AIEEE - 2012
- Mole concept and Molar Masses
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.
