Question:
The maximum area of a rectangle inscribed in the circle $(x + 1)^2 + (y - 3)^2 = 64$ is
The maximum area of a rectangle inscribed in the circle $(x + 1)^2 + (y - 3)^2 = 64$ is
Updated On: Oct 11, 2024
- 64 s units
- 72 s units
- 128 s units
- 8 s units
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The area of a rectangle inscribed in a circle is maximum, when it is a square
The area of a rectangle inscribed in a circle is maximum, when it is a square.
$\Rightarrow(\text { diagonal })^{2}=(\text { side })^{2}+(\text { side })^{2}$
$\Rightarrow$ (diameter) $^{2}=2$ (side) $^{2}$
(because diagonal = diameter)
$\Rightarrow \frac{(16)^{2}}{2}=(\text { side })^{2}$
$\therefore$ Area $=128$ s units
The area of a rectangle inscribed in a circle is maximum, when it is a square.
$\Rightarrow(\text { diagonal })^{2}=(\text { side })^{2}+(\text { side })^{2}$
$\Rightarrow$ (diameter) $^{2}=2$ (side) $^{2}$
(because diagonal = diameter)
$\Rightarrow \frac{(16)^{2}}{2}=(\text { side })^{2}$
$\therefore$ Area $=128$ s units
Was this answer helpful?
0
1
Top Questions on Approximations
Questions Asked in KCET exam
- The derivative of \( \sin x \) with respect to \( \log x \) is:
- KCET - 2025
- Derivatives
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- A horizontal pipe carries water in a streamlined flow. At a point along the pipe, where the cross-sectional area is \( 10 \, \text{cm}^2 \), the velocity of water is 1 m/s and the pressure is 2000 Pa. What is the pressure of water at another point where the cross-sectional area is \( 5 \, \text{cm}^2 \)? [Density of water = 1000 kg/m³]
- KCET - 2025
- Heat Transfer
- A series LCR circuit containing an AC source of 100V has an inductor and a capacitor of reactances 24\(\Omega\) and 16\(\Omega\) respectively. If a resistance of 6\(\Omega\) is connected in series, then the potential difference across the series combination of inductor and capacitor will be
- KCET - 2025
- Electromagnetic waves
- The correct statement/s about Galvanic cell is/are:
(a) Current flows from cathode to anode
(b) Anode is positive terminal
(c) If \(E_{\text{cell}} < 0\), then it is spontaneous reaction
(d) Cathode is positive terminal- KCET - 2025
- Electrochemistry
View More Questions
Concepts Used:
Approximations
The theory that is part of mathematics is the approximation theory. An approximation is employed when it becomes difficult to seek out the exact value of any number. It is also essential to round off the errors resulting in approximation.
Symbol of Approximation:
In general, the wavy equal “≈” sign is used to represent the approximate values that stand for “almost equal to”.
For Example ⇢ π ≈ 3.14
Approximations of Derivatives:
Consider y = f(x) = any function of x.
Let,
Δx = the small change in x
Δy = the corresponding change in y
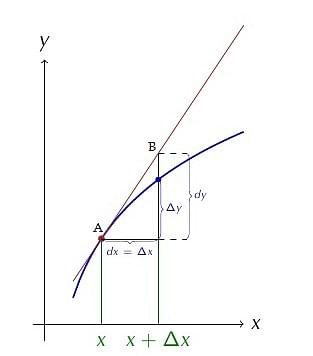
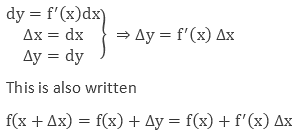
Here are some of the essential points that are required to be remembered:
- The differential of the dependent variable can not be equal to the increase of the variable whereas the differential of the independent variable can be equal to the increase of the variable.
- Absolute error in x is the change Δx.