Question:
The angle of intersection of the two curves $xy = a^2$ and $x^2 + y^2 = 2a^2$ is
The angle of intersection of the two curves $xy = a^2$ and $x^2 + y^2 = 2a^2$ is
Updated On: Jul 7, 2022
- $\frac {\pi} {6}$
- $\frac {\pi} {4}$
- $\frac {\pi} {3}$
- none of these
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
$xy = a^2$
$\Rightarrow y = \frac{a^{2}}{x}$
$\Rightarrow \frac{dy}{dx}=-\frac{a^{2}}{x^{2}}$
$x^{2}+y^{2} = 2a^{2}$
$\Rightarrow 2x + 2y \frac{dy}{dx}=0$
$\Rightarrow \frac{dy}{dx}=-\frac{x}{y}$.
Let $\left(x_{1}, y_{1}\right)$ be the pt. of intersection of the curves.
$\left(\frac{dy}{dx}\right)$ at $\left(x_{1}, y_{1}\right)$ for first curve $= - \frac{a^{2}}{x^{2}_{1}}$ and for second $= - \frac{x_{1}}{y_{1}}$.
Now $x^{2}_{1} + y^{2}_{1} = 2a^{2}, x_{1}y_{1} = a^{2}$
$\Rightarrow \left(x^{2}_{1}-y^{2}_{1}\right)^{2}=\left(x^{2}_{1}-y^{2}_{1}\right)^{2}-4\,x^{2}_{1}y^{2}_{1}$
$= 4a^{4} - 4a^{4} = 0$
$\Rightarrow x^{2}_{1}=y^{2}_{1}$
But $x^{2}_{1}+y^{2}_{1}=2a^{2}$
$\Rightarrow 2\,x^{2}_{1} = 2a^{2}$
$\Rightarrow x^{2}_{1} = a^{2}$
$\Rightarrow y^{2}_{1} = a^{2}$
$\therefore x_{1} = y_{1} = a$
$\therefore$ slopes of the two curves at $\left(x_{1}, y_{1}\right)$ are equal and is $- 1$.
$\therefore$ angle $= \pi$
Was this answer helpful?
0
0
Top Questions on Approximations
Concepts Used:
Approximations
The theory that is part of mathematics is the approximation theory. An approximation is employed when it becomes difficult to seek out the exact value of any number. It is also essential to round off the errors resulting in approximation.
Symbol of Approximation:
In general, the wavy equal “≈” sign is used to represent the approximate values that stand for “almost equal to”.
For Example ⇢ π ≈ 3.14
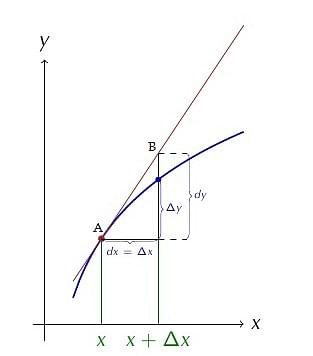
Approximations of Derivatives:
Consider y = f(x) = any function of x.
Let,
Δx = the small change in x
Δy = the corresponding change in y
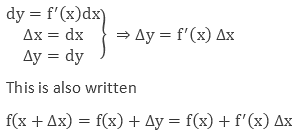
Here are some of the essential points that are required to be remembered:
- The differential of the dependent variable can not be equal to the increase of the variable whereas the differential of the independent variable can be equal to the increase of the variable.
- Absolute error in x is the change Δx.