The line through the points (h, 3) and (4, 1) intersects the line \(7x - 9y - 19 = 0\). at right angle. Find the value of h.
Solution and Explanation
The slope of the line passing through points (h, 3) and (4, 1) is \(m_1 = \frac{(1-3)}{(4-h)} = \frac{-2}{(4-h)}\)
The slope of line \(7x - 9y - 19 = 0\) or \(y = \frac{7}{9}x – \frac{19}{9} \) is \(m_2 =\frac{ 7}{9}\)
It is given that the two lines are perpendicular.
\(∴m_1 × m_2 = -1\)
\(⇒\frac{-2}{(4-h)} \times\frac{ 7}{9} = -1\)
\(⇒\frac{-14}{\left(36-9h\right)} = -1\)
\(⇒-14= -1\times(36 – 9h)\)
\(⇒36 – 9h = 14\)
\(⇒9h = 36 – 14\)
\(⇒h =\frac{ 22}{9}\)
Thus, the value of h is \(\frac{22}{9}.\)
Top Questions on Distance of a Point From a Line
- If the mirror image of the point \(P(3,4,9)\) in the Line
\(\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-2}{1}\) is \((α,β,γ)\) then find \(14(a+ẞ+y)\) is:- JEE Main - 2024
- Mathematics
- Distance of a Point From a Line
- If \(x^2-y^2+2hxy+2gx+2fy+c=0\) is the locus of points such that it is equidistant from the lines \(x+2y-8=0\) and \(2x+y+7=0\), then value of \(g+c+h-f\) is
- JEE Main - 2024
- Mathematics
- Distance of a Point From a Line
If \( (a, b) \) be the orthocenter of the triangle whose vertices are \( (1, 2) \), \( (2, 3) \), and \( (3, 1) \), and \( I_1 = \int_a^b x \sin(4x - x^2) dx \), \( I_2 = \int_a^b \sin(4x - x^2) dx \), then \( 36 \frac{I_1}{I_2} \) is equal to:
- JEE Main - 2024
- Mathematics
- Distance of a Point From a Line
- Let the point $P(\alpha, \beta)$ be at a unit distance from each of the two lines $L _1: 3 x -4 y +12=0$, and $L _2: 8 x +6 y +11=0$ If $P$ lies below $L _1$ and above $L _2$, then $100(\alpha+\beta)$ is equal to
- JEE Main - 2023
- Mathematics
- Distance of a Point From a Line
- In an isosceles triangle ABC, the vertex A is \((6, 1)\) and the equation of the base BC is \(2x + y = 4\). Let the point B lie on the line \(x + 3y = 7\). If \((α, β)\) is the centroid of ΔABC, then \(15(α + β)\) is equal to :
- JEE Main - 2022
- Mathematics
- Distance of a Point From a Line
Questions Asked in CBSE Class XI exam
- Draw formulas for the first five members of each homologous series beginning with the following compounds.\((a) H–COOH (b) CH_3COCH_3 (c) H–CH=CH_2\)
- CBSE Class XI
- Organic Chemistry- Some Basic Principles and Techniques
- Distinguish between the following pairs of sentences.
(i) He was visibly moved.
(ii) He was visually impaired.- CBSE Class XI
- The adventure
- How, according to you, can peace and liberty be maintained in a state?
- CBSE Class XI
- The tale of melon City
Figures 9.20(a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect ? Why ?
- CBSE Class XI
- Pressure
- Describe the change in hybridisation (if any) of the Al atom in the following reaction.
\(AlCl_3+Cl^- \rightarrow AlCl_4^-\)- CBSE Class XI
- Hybridisation
Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:
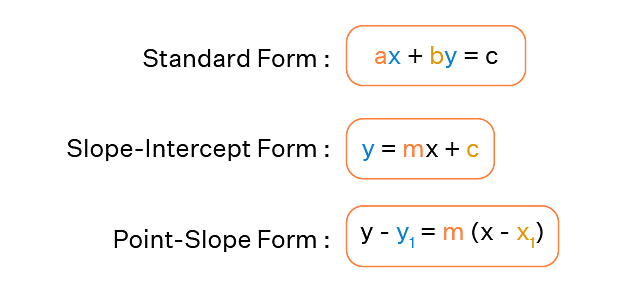
The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c