Question:
The length of a rubber cord is $ {{l}_{1}} $ metre when the tension is $ 4\, N $ and $ {{l}_{2}} $ metre when the tension is $ 6\, N $ . The length when the tension is $9\,N$, is
The length of a rubber cord is $ {{l}_{1}} $ metre when the tension is $ 4\, N $ and $ {{l}_{2}} $ metre when the tension is $ 6\, N $ . The length when the tension is $9\,N$, is
Updated On: Jun 4, 2024
- $ (2.5{{l}_{2}}-1.5{{l}_{1}})m $
- $ (6{{l}_{2}}-1.5{{l}_{1}})m $
- $ (3{{l}_{2}}-2{{l}_{1}})m $
- $ (3.5{{l}_{2}}-2.5{{l}_{1}})m $
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Let the original unstretched length be $ l. $
$ Y=\frac{Stress}{Strain}=\frac{T/A}{\Delta l/l}=\frac{T}{A}\times \frac{l}{\Delta l} $
Now $ Y=\frac{4}{A}\frac{l}{({{l}_{1}}-l)}=\frac{6}{A}\frac{l}{({{l}_{2}}-l)} $
$ =\frac{9}{A}\frac{l}{({{l}_{3}}-l)} $
$ \therefore $ $ 4({{l}_{3}}-l)=9({{l}_{1}}-l) $
$ \Rightarrow $ $ 4{{l}_{3}}+5l=9{{l}_{1}} $ .... (i)
Again, $ 6({{l}_{3}}-l)=9({{l}_{2}}-l) $
$ \Rightarrow $ $ 2{{l}_{3}}+l=3{{l}_{2}} $ ...(ii)
Solve Eqs. (i) and (ii), we obtain
$ {{l}_{3}}=(2.5{{l}_{2}}-1.5{{l}_{1}}) $
$ Y=\frac{Stress}{Strain}=\frac{T/A}{\Delta l/l}=\frac{T}{A}\times \frac{l}{\Delta l} $
Now $ Y=\frac{4}{A}\frac{l}{({{l}_{1}}-l)}=\frac{6}{A}\frac{l}{({{l}_{2}}-l)} $
$ =\frac{9}{A}\frac{l}{({{l}_{3}}-l)} $
$ \therefore $ $ 4({{l}_{3}}-l)=9({{l}_{1}}-l) $
$ \Rightarrow $ $ 4{{l}_{3}}+5l=9{{l}_{1}} $ .... (i)
Again, $ 6({{l}_{3}}-l)=9({{l}_{2}}-l) $
$ \Rightarrow $ $ 2{{l}_{3}}+l=3{{l}_{2}} $ ...(ii)
Solve Eqs. (i) and (ii), we obtain
$ {{l}_{3}}=(2.5{{l}_{2}}-1.5{{l}_{1}}) $
Was this answer helpful?
0
0
Top Questions on elastic moduli
- The slope of the stress-strain curve in the elastic deformation region is
- JKCET - 2024
- Physics
- elastic moduli
- The law which states that within elastic limits strain produced is proportional to the stress producing it is known as
- JKCET - 2024
- Physics
- elastic moduli
- A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5 cm. Another wire of the same material of length 4L and radius 4r is pulled by a force 4F under same conditions. The increase in length of this wire is ___ cm.
- JEE Main - 2022
- Physics
- elastic moduli
The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
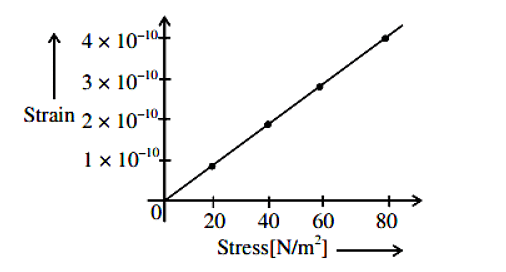
- JEE Main - 2022
- Physics
- elastic moduli
- If the length of a wire is made double and radius is halved of its respective values. Then, the Young’s modulus of the material of the wire will :
- JEE Main - 2022
- Physics
- elastic moduli
View More Questions
Questions Asked in KEAM exam
- Which among the following has the highest molar elevation constant?
- KEAM - 2025
- Colligative Properties
- The formula of Ammonium phosphomolybdate is
- KEAM - 2025
- coordination compounds
- Which is a Lewis acid?
- KEAM - 2025
- Acids and Bases
- Hardness of water is estimated by titration with
- KEAM - 2025
- Solutions
- Which of the following gases has the lowest solubility in water at 298 K?
- KEAM - 2025
- Solutions
View More Questions