Question:
The inversion temperature for a van der Waals gas is given by:
The inversion temperature for a van der Waals gas is given by:
Updated On: Jun 7, 2022
- $ {{T}_{i}}=\frac{2a}{Rb} $
- $ {{T}_{i}}=\frac{a}{Rb} $
- $ {{T}_{i}}=\frac{a}{2Rb} $
- $ {{T}_{i}}=0.5\,{{T}_{Boyle}} $
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Inversion temperature of a van der Waals gas is given by $ {{T}_{i}}=\frac{2a}{Rb}=2{{T}_{b}} $ (where $ {{T}_{b}}= $ Boyle temperature)
Was this answer helpful?
0
0
Top Questions on Van Der Waals equation
- Which of the following statemnt is incorect for physisorption?
- GUJCET - 2023
- Chemistry
- Van Der Waals equation
- Arrange the following gases in increasing order of van der Waals constant 'a'
A. Ar
B. CH4
C. H₂O
D. C6H6
Choose the correct option from the following.- JEE Main - 2023
- Chemistry
- Van Der Waals equation
- At low pressure, the van der Waal's equation is reduced to
- VITEEE - 2019
- Chemistry
- Van Der Waals equation
- Given van der Waals constant for NH3, H2, O2 and CO2 are respectively 4.17, 0.244, 1.36 and 3.59, which one of the following gases is most easily liquefied ?
- NEET (UG) - 2018
- Chemistry
- Van Der Waals equation
- If $V$ is the volume of one molecule of gas under given conditions, the van der Waal?s constant $b$ is
- BITSAT - 2018
- Chemistry
- Van Der Waals equation
View More Questions
Questions Asked in JIPMER exam
- Binomial nomenclature was first introduced by
- JIPMER - 2015
- KCET - 2022
- Diversity In The Living World
- A convex lens $'A'$ of focal length $20\, cm$ and a concave lens $'B'$ of focal length $5\, cm$ are kept along the same axis with a distance $'d'$ between them. If a parallel beam of light falling on $'A'$ leaves $'B'$ as a parallel beam, then the distance $'d'$ in cm will be :
- JIPMER - 2021
- Spherical Mirrors
- A bacterial flagellum is composed of
- JIPMER - 2021
- Prokaryotic Cells
- $2,4-DNP $ test can be used to identify :
- JIPMER - 2021
- Chemical Reactions
- How many moles of acidified $K_2Cr_2O_7$ is required to liberate $6$ moles of $I_2$ from an aqueous solution of $I^-$ ?
- JIPMER - 2020
- Mole concept and Molar Masses
View More Questions
Concepts Used:
Van Der Waals Equation
Van der Waals equation is an equation relating the relationship between the pressure, volume, temperature, and amount of real gases.
Read More: Derivation of Van Der Waals Equation
Derivation of Van der Waals equation:
For a real gas containing ‘n’ moles, the equation is written as
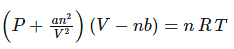
Where, P, V, T, n are the pressure, volume, temperature and moles of the gas. ‘a’ and ‘b’ constants specific to each gas.
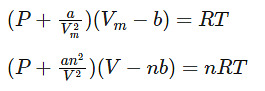
Where,
Vm: molar volume of the gas
R: universal gas constant
T: temperature
P: pressure
V: volume
Thus, Van der Waals equation can be reduced to ideal gas law as PVm = RT.
The equation can further be written as;
- Cube power of volume:
- Reduced equation (Law of corresponding states) in terms of critical constants:
Units of Van der Waals equation Constants
a: atm lit² mol-²
b: litre mol-¹