The following figure shows a beam of light converging at point \(P\). When a concave lens of focal length \(16 \,cm\) is introduced in the path of the beam at a place shown by dotted line such that \(OP\) becomes the axis of the lens, the beam converges at a distance \(x\) from the lens. The value of \(x\) will be equal to


- 12 cm
- 24 cm
- 36 cm
- 48 cm
The Correct Option is D
Approach Solution - 1
let the beam will converge at a distance \(x=v\)
Using lens formulae, we have, \(\frac{1}{f} = \frac{1}{v} - \frac{1}{u}\)
Where \(u =12\, cm\) and \(f =-16\, cm\) is given
\(\therefore \frac{1}{v} = \frac{1}{f} + \frac{1}{u}\)
\(\left( -\frac{1}{16} \right) + \left( \frac{1}{12} \right) = \frac{1}{48} \, \text{cm}\)
\(\Rightarrow v =48 \,cm\)
Hence, \(x=48 \,cm\)
Approach Solution -2
For a concave lens, the focal length \(f\) is negative. The formula for the image distance \(v\) formed by a lens is given by the lens equation: \[ \frac{1}{f} = \frac{1}{u} + \frac{1}{v} \] Where:
\(f\) is the focal length of the lens,
\(u\) is the object distance (distance from the lens to the point where the light beam converges),
\(v\) is the image distance (the distance at which the beam will converge after passing through the lens).
In this case, \(f = -16\) cm (since the lens is concave), and the object distance \(u = -12\) cm (since the beam converges at point P).
Substituting into the lens formula: \[ \frac{1}{-16} = \frac{1}{-12} + \frac{1}{v} \] Solving for \(v\), we get: \[ v = 48 \, \text{cm} \] Thus, the beam will converge at a distance of 48 cm from the lens.
Approach Solution -3
This is a problem involving a concave lens. When a converging beam of light passes through a concave lens, the lens diverges the light, and the focal point shifts based on the lens's focal length. The focal length \( f \) of the concave lens is given as 16 cm, and the beam converges at point P when the lens is placed along the path of the beam. The light initially converges at point P at a distance of 12 cm from the lens (OP = 12 cm). To calculate the new convergence point, we use the lens formula: \[ \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \] Where:
\( f \) is the focal length of the lens,
\( v \) is the image distance (the distance at which the beam converges after passing through the lens),
\( u \) is the object distance (the initial distance at which the beam converges before passing through the lens).
The object distance \( u \) is -12 cm (since the beam converges at point P, which is 12 cm from the lens). The focal length \( f \) is -16 cm (since it's a concave lens). Substituting the known values into the lens formula: \[ \frac{1}{-16} = \frac{1}{v} - \frac{1}{-12} \] Solving for \( v \): \[ \frac{1}{v} = \frac{1}{-16} + \frac{1}{12} \] \[ \frac{1}{v} = \frac{-3 + 4}{48} = \frac{1}{48} \] \[ v = 48 \, \text{cm} \] Thus, the distance \( x \) from the lens where the beam converges is 48 cm.
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in KCET exam
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- A random experiment has five outcomes \(w_1, w_2, w_3, w_4, w_5\). The probabilities of the occurrence of the outcomes \(w_1, w_2, w_4, w_5\) are respectively \( \frac{1}{6}, a, b, \frac{1}{12} \) such that \(12a + 12b - 1 = 0\). Then the probabilities of occurrence of the outcome \(w_3\) is:
- KCET - 2025
- Probability
- If 'a' and 'b' are the order and degree respectively of the differentiable equation \[ \frac{d^2 y}{dx^2} + \left(\frac{dy}{dx}\right)^3 + x^4 = 0, \quad \text{then} \, a - b = \, \_ \_ \]
- KCET - 2025
- Differential equations
- Meera visits only one of the two temples A and B in her locality. Probability that she visits temple A is \( \frac{2}{5} \). If she visits temple A, the probability that she meets her friend is \( \frac{1}{3} \). The probability that she meets her friend, whereas it is \( \frac{2}{7} \) if she visits temple B. Meera met her friend at one of the two temples. The probability that she met her friend at temple B is:
- KCET - 2025
- Probability
In a practical examination, the following pedigree chart was given as a spotter for identification. The students identify the given pedigree chart as

- KCET - 2025
- Genetics
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
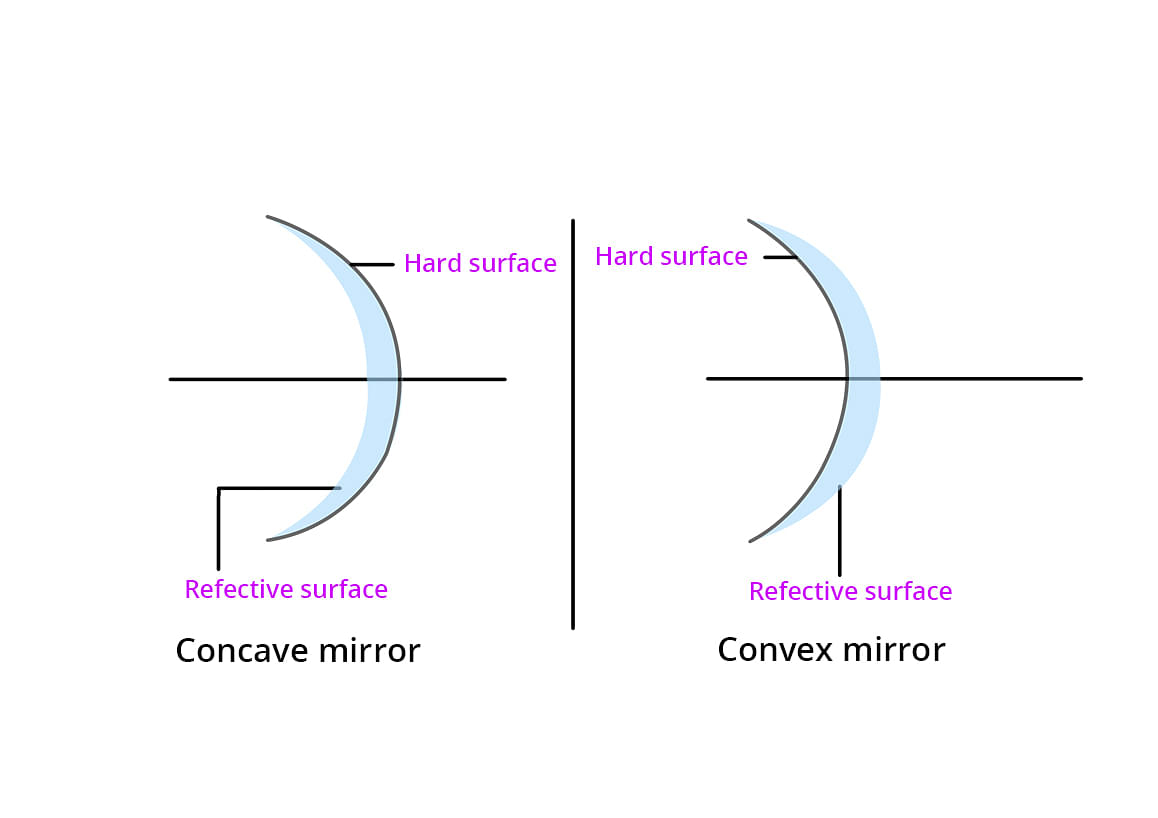
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.