Comprehension
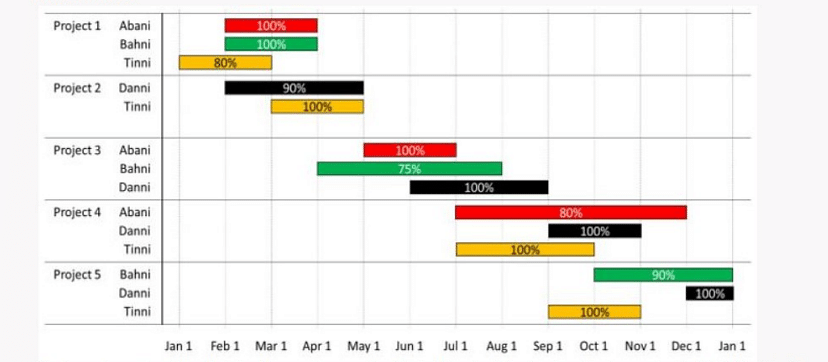
The figure above shows the schedule of four employees – Abani, Bahni, Danni and Tinni –whom Dhoni supervised in 2020. Altogether there were five projects which started and concluded in 2020 in which they were involved. For each of these projects and for each employee, the starting day was at the beginning of a month and the concluding day was the end of a month, and these are indicated by the left and right end points of the corresponding horizontal bars. The number within each bar indicates the percentage of assigned work completed by the employee for that project, as assessed by Dhoni.For each employee, his/her total project-month (in 2020) is the sum of the number of months(s)he worked across the five project, while his/her annual completion index is the weightage average of the completion percentage assigned from the different projects, with the weights being the corresponding number of months (s)he worked in these projects. For each project, the total employee-month is the sum of the number of months four employees worked in this project, while its completion index is the weightage average of the completion percentage assigned for the employees who worked in this project, with the weights being the corresponding number of months they worked in this project.
Question: 1
Which of the following statements is/are true?
I: The total project-month was the same for the four employees.
II: The total employee-month was the same for the five projects.
Which of the following statements is/are true?
I: The total project-month was the same for the four employees.
II: The total employee-month was the same for the five projects.
I: The total project-month was the same for the four employees.
II: The total employee-month was the same for the five projects.
Updated On: Aug 20, 2024
- Only I
- Both I and II
- Only II
- Neither I nor II
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
The correct answer is (A): Only I
Was this answer helpful?
0
0
Question: 2
Which employees did not work in multiple projects for any of the months in 2020?
Which employees did not work in multiple projects for any of the months in 2020?
Updated On: Aug 20, 2024
- All four of them
- Only Tinni
- Only Abani and Bahni
- Only Abani, Bahni and Danni
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
The correct answer is (D);
Only Abani, Bahni and Danni
Only Abani, Bahni and Danni
Was this answer helpful?
0
0
Question: 3
The project duration, measured in terms of the number of months, is the time during which at least one employee worked in the project. Which of the following pairs of the projects had the same duration?
The project duration, measured in terms of the number of months, is the time during which at least one employee worked in the project. Which of the following pairs of the projects had the same duration?
Updated On: Aug 20, 2024
- Project 3, Project 5
- Project 4, Project 5
- Project 1, Project 5
- Project 3, Project 4
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
The correct answer is (D) Project 3, Project 4
Was this answer helpful?
0
0
Question: 4
The list of employees in decreasing order of annual completion index is:
The list of employees in decreasing order of annual completion index is:
Updated On: Aug 20, 2024
- Danni, Tinni, Bahni, Abani
- Danni, Tinni, Abani, Bahni
- Bahni, Abani, Tinni, Danni
- Tinni, Danni, Abani, Bahni
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The correct answer is (B): Danni, Tinni, Abani, Bahni
Was this answer helpful?
0
0
Top Questions on Data Interpretation
The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.- CAT - 2024
- Data Interpretation & Logical Reasoning (DILR)
- Data Interpretation
- Two students, Amiya and Ramya are the only candidates in an election for the position of class representative. Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
• The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. For example, if Amiya and Ramya both run vigorous campaigns, then $20 × (2+2)\%$, that is, $80\%$ of the students will vote in the election.
• Among voting students, the percentage of votes for each candidate will be proportional to the levels of their campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2) campaign, then Amiya will receive \(\frac{1}{3}\) of the votes cast, and Ramya will receive the other \(\frac{2}{3}\).
The above-mentioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
• If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then $10\%$ of the students who would have otherwise voted for Amiya will vote for Ramya, and another $10\%$ who would have otherwise voted for Amiya, will not vote at all.
• If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then $20\%$ of the students who would have otherwise voted for Ramya will vote for Amiya, and another $5\%$ who would have otherwise voted for Ramya, will not vote at all.
• If both run campaigns attacking each other, then $10\%$ of the students who would have otherwise voted for them had they run campaigns focusing on issues, will not vote at all.- CAT - 2024
- Data Interpretation & Logical Reasoning (DILR)
- Data Interpretation
- Read the Passage carefully and answer the following questions.
An air conditioner (AC) unit has three operating modes: Eco, Normal, and Turbo. The power consumption in each mode is as follows: Eco mode consumes 1000 watts, Normal mode consumes 1200 watts, and Turbo mode consumes 1500 watts. Yesterday, the AC was in operation from 2 PM to 10 PM. From 2 PM to 6 PM it ran in Eco mode. From 6 PM to 8 PM, it ran in Normal mode. From 8 PM to 10 PM it ran in Turbo mode.- CAT - 2024
- Data Interpretation & Logical Reasoning (DILR)
- Data Interpretation
- Read the Passage carefully and answer the following questions
A health food store specializing in dietary supplements and whole grains recorded the following sales figures (in kilograms) for various food categories last month: Millets (M) = 500 kg at a cost price of 40/kg and selling price of 50/kg; Protein supplements (P) = 300 kg at a cost price of 80/kg and selling price of 100/kg; Vitamin supplements (V) = 200 kg at a cost price of 60/kg and selling price of 80/kg; Carbohydrates (C) = 600 kg at a cost price of 80/kg and selling price of 100/kg; Fats (F) = 100 kg at a cost price of 120/kg and selling price of 150/kg. Additionally, they sold 50 kg of mixed nuts (N) at a cost price of 100/kg and a selling price of 130/kg- CAT - 2024
- Data Interpretation & Logical Reasoning (DILR)
- Data Interpretation
- In a class of 40 students, the ratio of boys to girls is 3:2. The average marks scored by boys is 42, and that by girls is 46. What is the average marks scored by the whole class?
- CUET (UG) - 2024
- General Aptitude
- Data Interpretation
View More Questions
Questions Asked in CAT exam
- The sum of all real values of $k$ for which $(\frac{1}{8})^k \times (\frac{1}{32768})^{\frac{4}{3}} = \frac{1}{8} \times (\frac{1}{32768})^{\frac{k}{3}}$ is
- CAT - 2024
- Logarithms
- Amal and Vimal together can complete a task in 150 days, while Vimal and Sunil together can complete the same task in 100 days. Amal starts working on the task and works for 75 days, then Vimal takes over and works for 135 days. Finally, Sunil takes over and completes the remaining task in 45 days. If Amal had started the task alone and worked on all days, Vimal had worked on every second day, and Sunil had worked on every third day, then the number of days required to complete the task would have been
- CAT - 2024
- Time and Work
- Gopi marks a price on a product in order to make 20% profit. Ravi gets 10% discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is
- CAT - 2024
- Profit and Loss
- Sam can complete a job in 20 days when working alone. Mohit is twice as fast as Sam and thrice as fast as Ayana in the same job. They undertake a job with an arrangement where Sam and Mohit work together on the first day, Sam and Ayana on the second day, Mohit and Ayana on the third day, and this three-day pattern is repeated till the work gets completed. Then, the fraction of total work done by Sam is
- CAT - 2024
- Time and Work
- The number of all positive integers up to 500 with non-repeating digits is
- CAT - 2024
- Number Systems
View More Questions