Question:
The amplitude of a wave disturbance propagating in positive direction of $x-axis$ is given by $y=\frac{1}{1 + x^{2}}$ at $t=0$ and by $y=\frac{1}{1 + \left(x - 1\right)^{2}}$ at $t=2 \, s$ , where $x \, $ and $y$ are in meters. The shape of the wave disturbance does not change during propagation. The velocity of the wave is
The amplitude of a wave disturbance propagating in positive direction of $x-axis$ is given by $y=\frac{1}{1 + x^{2}}$ at $t=0$ and by $y=\frac{1}{1 + \left(x - 1\right)^{2}}$ at $t=2 \, s$ , where $x \, $ and $y$ are in meters. The shape of the wave disturbance does not change during propagation. The velocity of the wave is
Updated On: Jul 28, 2022
- $0.5ms^{- 1}$
- $2.0ms^{- 1}$
- $1.0ms^{- 1}$
- $4.0ms^{- 1}$
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
In a wave equation, $x$ and $t$ must be related in the form $\left(\right.x-vt\left.\right)$ . Therefore, we rewrite the given equation as
$y=\frac{1}{1 + \left(x - v t\right)^{2}}$
For $t=0,$ it becomes $y=\frac{1}{1 + x^{2}}$
And for $t=2$ , it becomes
$y=\frac{1}{\left[1 + \left(x - 2 v\right)^{2}\right]}=\frac{1}{1 + \left(x - 1\right)^{2}}$
$\therefore 2v=1$ or $v=0.5 \, ms^{- 1}$
Was this answer helpful?
0
0
Top Questions on doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
- When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
- AP EAPCET - 2025
- Physics
- doppler effect
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
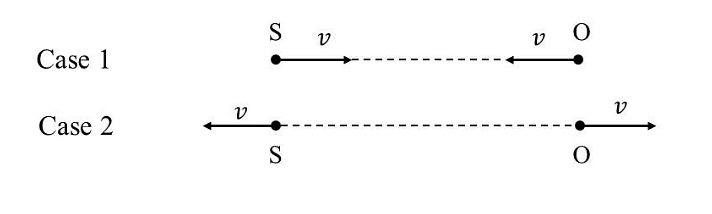
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
View More Questions
Concepts Used:
Doppler Effect
The Doppler effect is a phenomenon caused by a moving wave source that causes an apparent upward shift in frequency for observers who are approaching the source and a visible downward change in frequency for observers who are retreating from the source. It's crucial to note that the impact isn't caused by a change in the source's frequency.

The Doppler effect may be seen in any wave type, including water waves, sound waves, and light waves. We are most familiar with the Doppler effect because of our encounters with sound waves