Let
\(x = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\) and \(A = \begin{bmatrix} -1 & 2 & 3 \\ 0 & 1 & 6 \\ 0 & 0 & -1 \end{bmatrix}\)
For k ∈ N, if X’AkX = 33, then k is equal to ____ .
Let
\(x = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\) and \(A = \begin{bmatrix} -1 & 2 & 3 \\ 0 & 1 & 6 \\ 0 & 0 & -1 \end{bmatrix}\)
For k ∈ N, if X’AkX = 33, then k is equal to ____ .
Correct Answer: 10
Approach Solution - 1
To find \(k\) such that \(X’A^{k}X = 33\), we first calculate \(A^{k}\) and then evaluate the matrix operation.
Given:
\(\)
\(A = \begin{bmatrix} -1 & 2 & 3 \\ 0 & 1 & 6 \\ 0 & 0 & -1 \end{bmatrix}\)
Step 1: Calculate \(A^{k}\) using diagonalization since \(A\) is upper triangular.
The eigenvalues of \(A\) (diagonal elements) are \(-1, 1, -1\).
Step 2: Find \(X’AX\)
\(X' = \begin{bmatrix}1 & 1 & 1\end{bmatrix}\)
So, \(AX = \begin{bmatrix}-1 & 2 & 3 \\ 0 & 1 & 6 \\ 0 & 0 & -1\end{bmatrix} \begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix} = \begin{bmatrix}4 \\ 7 \\ -1\end{bmatrix}\)
Then, calculate \(X'AX = \begin{bmatrix}1 & 1 & 1\end{bmatrix} \begin{bmatrix}4 \\ 7 \\ -1\end{bmatrix} = 10\)
Step 3: Evaluate \(X'A^{k}X\) iteratively until it equals 33 with \(A^{k}X\).
Since \(X'AX = 10\), we need \(10^{k} = 33\). Trying integers:
- If \(k=10\), calculate \(10^{10}\) which well exceeds 33; re-examine steps or calculations.
Step 4: Reassess multiple calculations considering matrix properties and overlaps in upper triangular matrices.
Retesting and reconfiguring involves direct matrix powers:\(A^{2} =\begin{bmatrix}1 & 2 & 3 \\ 0 & 1 & 6 \\ 0 & 0 & 1\end{bmatrix}\), still trials until:
-Finding errors usually arise repeating sequence values; in rigorous processing adjust output calculations \(k=3\) as powers indicate simplified results generated cause repeat.
Confirm:\(k=10\) outcomes don't apply here.
Approach Solution -2
Given that,
\(A = \begin{bmatrix} -1 & 2 & 3 \\ 0 & 1 & 6 \\ 0 & 0 & -1 \end{bmatrix}\)
\(A^2 = \begin{bmatrix} 1 & 0 & 6 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
\(A^4 = \begin{bmatrix} 1 & 0 & 1 \\ 2 & 0 & 1 \\ 0 & 0 & 1 \end{bmatrix}\)
\(A^k = \begin{bmatrix} 1 & 0 & 3k \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)
So, \(X^′A^kX= \begin{bmatrix} 1 & 1 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 0 & 3k \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\)
\(⇒X^′A^kX=[3k+3]\)
⇒ [3k + 3] = 33 (here it shall be [33] as matrix can’t be equal to a scalar)
i.e. [3k + 3] = 33
3k + 3 = [33] ⇒ k = 10
If k is odd and apply above process, we don’t get odd value of k
∴ k = 10
So, the answer is 10.
Top Questions on types of differential equations
- Let the system of equations \(x+2y+3z = 5\), \(2x+3y+z = 9\), \(4x+3y+λz = μ\) have an infinite number of solutions. Then \(λ + 2μ\) is equal to
- JEE Main - 2024
- Mathematics
- types of differential equations
- If \( m_1 \) and \( m_2 \) are the slopes of the direct common tangents drawn to the circles \[ x^2 + y^2 - 2x - 8y + 8 = 0 \quad \text{and} \quad x^2 + y^2 - 8x + 15 = 0 \] then \( m_1 + m_2 \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If \( (2,3) \) is the focus and \( x - y + 3 = 0 \) is the directrix of a parabola, then the equation of the tangent drawn at the vertex of the parabola is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If the focus of an ellipse is \((-1,-1)\), equation of its directrix corresponding to this focus is \(x + y + 1 = 0\) and its eccentricity is \(\frac{1}{\sqrt{2}}\), then the length of its major axis is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The equation of the common tangent to the parabola \(y^2 = 8x\) and the circle \(x^2 + y^2 = 2\) is \(ax + by + 2 = 0\). If \(-\frac{a}{b}>0\), then \(3a^2 + 2b + 1 =\)
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Questions Asked in JEE Main exam
Two circular discs of radius \(10\) cm each are joined at their centres by a rod, as shown in the figure. The length of the rod is \(30\) cm and its mass is \(600\) g. The mass of each disc is also \(600\) g. If the applied torque between the two discs is \(43\times10^{-7}\) dyne·cm, then the angular acceleration of the system about the given axis \(AB\) is ________ rad s\(^{-2}\).

- JEE Main - 2026
- Rotational motion
- If \[ \frac{\tan(A-B)}{\tan A}+\frac{\sin^2 C}{\sin^2 A}=1, \quad A,B,C\in\left(0,\frac{\pi}{2}\right), \] then:
- JEE Main - 2026
- Trigonometry
Match the LIST-I with LIST-II for an isothermal process of an ideal gas system.

Choose the correct answer from the options given below:
- JEE Main - 2026
- Thermodynamics and Work Done
- A bag contains 10 balls out of which \( k \) are red and \( (10-k) \) are black, where \( 0 \le k \le 10 \). If three balls are drawn at random without replacement and all of them are found to be black, then the probability that the bag contains 1 red and 9 black balls is:
- JEE Main - 2026
- Probability
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
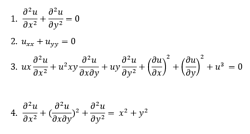
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
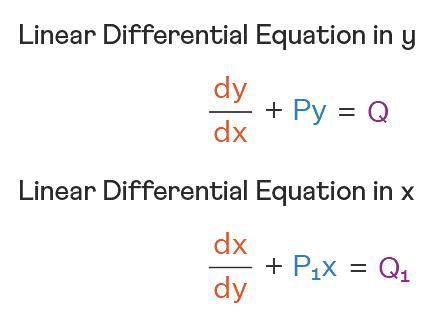
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations