Let $S_1 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≥ x^2, x, y ≥ 0}$ and $S_2 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≤ x^2, x, y ≥ 0}.$ Then, which of the following is CORRECT ?
Show Hint
- Both $S_1$ and $S_2$ are convex sets
- $S_1$ is a convex set but $S_2$ is not a convex set
- $S_1$ is a convex set but $S_2$ is not a convex set
- Neither $S_1$ nor $S_2$ are convex sets
The Correct Option is B
Solution and Explanation
Convexity Analysis of Regions S₁ and S₂
The convexity of a set is determined by whether the line segment between any two points in the set remains entirely within the set.
Region S₁: y ≥ x²
The region S₁ is defined by the constraint:
y ≥ x²
This means that S₁ includes all points above the parabola y = x². Despite the presence of x², which often suggests non-convexity, this region remains convex because any line segment drawn between two points within S₁ remains within the set.
Region S₂: y ≤ x²
The region S₂ is defined by the constraint:
y ≤ x²
Here, S₂ includes all points below the parabola y = x². However, this region is non-convex because the parabolic curve y = x² creates gaps where line segments between two points in S₂ can extend outside the region.
Conclusion:
- S₁ (y ≥ x²) is convex since it includes all line segments between any two points within the set.
- S₂ (y ≤ x²) is non-convex because certain line segments between points in S₂ extend outside the region.
Top Questions on Sets
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
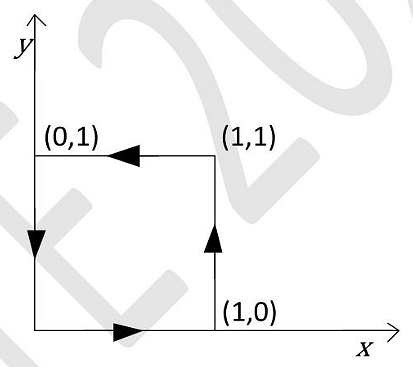
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
Questions Asked in IIT JAM EN exam
- Consider the matrix \( A = \begin{bmatrix} 4 & -1 \\ 12 & -3 \end{bmatrix} \).
The value of the determinant of \( A^5 \) is .......... (rounded off to two decimal places).- IIT JAM EN - 2025
- Linear Algebra
The sum of the payoffs to the players in the Nash equilibrium of the following simultaneous game is ............
Player Y C NC Player X X: 50, Y: 50 X: 40, Y: 30 X: 30, Y: 40 X: 20, Y: 20 - IIT JAM EN - 2025
- Economics and economic theories
- Consider the economy described by the following: \[ Y = C + I + G \quad \text{with} \quad Y = 5000, \, G = 1000, \, T = 1000, \quad \text{and} \quad C = 250 + 0.75(Y - T), \] where \( Y \), \( C \), \( I \), \( G \), and \( T \) are national income, private consumption spending, investment expenditure, government expenditure, and tax revenue respectively. In this economy, private saving is ............
- IIT JAM EN - 2025
- Microeconomics
- Lerner Index (\( L \)), a measure of market power, is defined as \( L = \frac{P - MC}{P} \), where \( P \) and \( MC \) are, respectively, price and marginal cost of a firm. If a profit maximizing firm faces the demand curve \( P^2 Q = 7 \), the value of \( L \) is ............ (rounded off to one decimal place).
- IIT JAM EN - 2025
- Microeconomics
- You are tossing a fair coin repeatedly until a ‘Head’ appears. The expected number of tosses required for a ‘Head’ to appear is ...........
- IIT JAM EN - 2025
- Probability