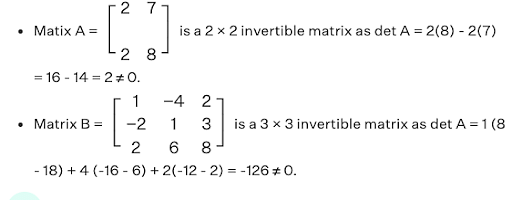Question:
Let A=$\begin{bmatrix}
1 & 3 & 2 \\
2 & 5 &t \\
4&7-t&-6 \\ \end{bmatrix}$, then the values of t for which inverse of A does not exist
Let A=$\begin{bmatrix}
1 & 3 & 2 \\
2 & 5 &t \\
4&7-t&-6 \\ \end{bmatrix}$, then the values of t for which inverse of A does not exist
Updated On: Feb 15, 2025
- -2, 1
- 44622
- 2, -3
- 3, -1
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
We know that inverse of A does not exist
only when |A| = 0
$\therefore$ $\begin{vmatrix}
1 & 3 & 2 \\
2 & 5 &t \\
4&7-t&-6 \\ \end{vmatrix}$=0
$(-30-7t+t^2)-3(-12-4t)$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +2(14-2t-20)=0 $
$\Rightarrow \ \ -30- 7t + t^2 +36+12t-12-4t=0$
$\Rightarrow \ \ t^2+t-6=0 \Rightarrow \ \ t^2 +3t \ -2t-6=0$
$\Rightarrow \ \ t(t+3)-2(t+3)=0$
$\Rightarrow \ \ \ \ (t+3)(t-2)=0 \ \Rightarrow \ t=2, -3$
only when |A| = 0
$\therefore$ $\begin{vmatrix}
1 & 3 & 2 \\
2 & 5 &t \\
4&7-t&-6 \\ \end{vmatrix}$=0
$(-30-7t+t^2)-3(-12-4t)$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +2(14-2t-20)=0 $
$\Rightarrow \ \ -30- 7t + t^2 +36+12t-12-4t=0$
$\Rightarrow \ \ t^2+t-6=0 \Rightarrow \ \ t^2 +3t \ -2t-6=0$
$\Rightarrow \ \ t(t+3)-2(t+3)=0$
$\Rightarrow \ \ \ \ (t+3)(t-2)=0 \ \Rightarrow \ t=2, -3$
Was this answer helpful?
0
0
Top Questions on Invertible Matrices
- If A is a non-identity invertible symmetric matrix, then \(A^{-1}\) is:
- CUET (UG) - 2023
- Mathematics
- Invertible Matrices
- The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- Which of the following matrices can NOT be obtained from the matrix \(\begin{bmatrix} -1 &2 \\ 1 & -1 \end{bmatrix}\) by a single elementary row operation?
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- If A and B are invertible matrices then which of the following is not correct ?
- KCET - 2021
- Mathematics
- Invertible Matrices
- The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
- KCET - 2019
- Mathematics
- Invertible Matrices
View More Questions
Questions Asked in VITEEE exam
- Images of consonants of the capital English alphabets are observed in a mirror. What is the number of images of these which look like their original shapes?
- VITEEE - 2025
- Logical Reasoning
- Data Interpretation: The following table shows the number of students in five different colleges. Answer the questions based on the data. \[ \begin{array}{|c|c|} \hline \text{College} & \text{Number of Students} \\ \hline \text{A} & 1000 \\ \text{B} & 1500 \\ \text{C} & 1200 \\ \text{D} & 1300 \\ \text{E} & 900 \\ \hline \end{array} \] Question: What is the average number of students in all five colleges?
- VITEEE - 2025
- Logical Reasoning
- Find the value of \( x \) in the equation \( 4(x - 2) = 3(x + 5) \).
- VITEEE - 2025
- Linear Equations
- A body of mass 10 kg is moving with a velocity of 20 m/s. What is the kinetic energy of the body?
- VITEEE - 2025
- Work Power and Energy
- What is the resistance of a conductor if the potential difference across it is 12 V and the current flowing through it is 3 A?
- VITEEE - 2025
- Resistance
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.