Question:
Let π1,π2, β¦ be a sequence of independent random variables such that
\(p(x_i=1)=\frac{1}{4}\) and \(p(x_i=21)=\frac{3}{4}\) i=1,2,β¦.
For some real constants π1 and π2, suppose that
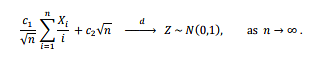
Then, the value of \(\sqrt{3}\) (3π1+π2) equals
Let π1,π2, β¦ be a sequence of independent random variables such that
\(p(x_i=1)=\frac{1}{4}\) and \(p(x_i=21)=\frac{3}{4}\) i=1,2,β¦.
For some real constants π1 and π2, suppose that
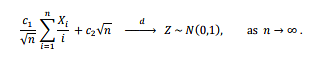
Then, the value of \(\sqrt{3}\) (3π1+π2) equals
\(p(x_i=1)=\frac{1}{4}\) and \(p(x_i=21)=\frac{3}{4}\) i=1,2,β¦.
For some real constants π1 and π2, suppose that
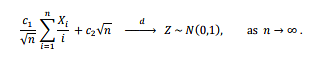
Then, the value of \(\sqrt{3}\) (3π1+π2) equals
Updated On: Oct 1, 2024
- 2
- 3
- 4
- 5
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
The correct option is (D): 5
Was this answer helpful?
0
0
Top Questions on Probability
- Two friends were born in the year 2000. The probability that they have the same birthday is :
- CBSE Class X - 2024
- Mathematics
- Probability
- A box contains cards numbered 6 to 50. A card is drawn at random from the box. The probability that the drawn card has a number which is a perfect square, is :
- CBSE Class X - 2024
- Mathematics
- Probability
- The probability of getting a sum of 8, when two dice are thrown simultaneously, is :
- CBSE Class X - 2024
- Mathematics
- Probability
- A bag contains 4 red, 5 white, and some yellow balls. If the probability of drawing a red ball at random is \(\frac{1}{5}\), then find the probability of drawing a yellow ball at random.
- CBSE Class X - 2024
- Mathematics
- Probability
- Two dice are rolled together. The probability of getting a doublet is:
- CBSE Class X - 2024
- Mathematics
- Probability
View More Questions
Questions Asked in IIT JAM MS exam
- Let \( f(x, y) = |xy| + x \) for all \( (x, y) \in \mathbb{R}^2 \). Determine the existence of the partial derivative of \( f \) with respect to \( x \) exists:
- IIT JAM MS - 2024
- Differential Calculus
- Let \( f(x) = 4x^2 - \sin x + \cos 2x \) for all \( x \in \mathbb{R} \). Determine the properties of the function \( f \):
- IIT JAM MS - 2024
- Differential Calculus
- For \( n \in \mathbb{N} \), let \[a_n = \sqrt{n} \sin^2\left(\frac{1}{n}\right) \cos n,\] and \[b_n = \sqrt{n} \sin\left(\frac{1}{n^2}\right) \cos n.\] Then
- IIT JAM MS - 2024
- Differential Calculus
- Let \( V = \{ (x_1, x_2, x_3, x_4) \in \mathbb{R}^4 \mid x_1 = x_2 \} \). Consider \( V \) as a subspace of \(\mathbb{R}^4\) over the real field. Then the dimension of \( V \) is equal to __________ (answer in integer).
- IIT JAM MS - 2024
- Differential Calculus
- Let \( \Omega = \{1,2,3,4,5,6\} \). Then which of the following classes of sets is an algebra?
- IIT JAM MS - 2024
- Differential Calculus
View More Questions