Question

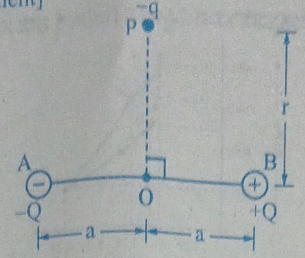
In the situation shown in the diagram, magnitude of q << | Q | and r>>a. The net force on the free charge -q and net torque on it about O at the instant shown are respectively
[ p = 2aQ is the dipole moment ]

• A. \(\frac{1}{4\pi\epsilon_0}\frac{pq}{r^2}\hat{k},\frac{1}{4\pi\epsilon_0}\frac{pq}{r^3}\hat{i}\)
• B. \(-\frac{1}{4\pi\epsilon_0}\frac{pq}{r^2}\hat{k},-\frac{1}{4\pi\epsilon_0}\frac{pq}{r^3}\hat{i}\)
• C. \(\frac{1}{4\pi\epsilon_0}\frac{pq}{r^3}\hat{i},+\frac{1}{4\pi\epsilon_0}\frac{pq}{r^2}\hat{k}\)
• D. \(\frac{1}{4\pi\epsilon_0}\frac{pq}{r^3}\hat{i},-\frac{1}{4\pi\epsilon_0}\frac{pq}{r^2}\hat{k}\)

Answer 1

The Correct Option is D

Given:

• Charge \( q \) is much smaller than \( |Q| \). 
• Distance \( r \gg a \).
• Dipole moment \( p = 2aQ \).

Step 1: Finding the Net Force on Charge \(-q\)

The force on a charge due to a dipole at a large distance \( r \) is given by:

\[ \mathbf{F} = \frac{1}{4\pi\epsilon_0} \frac{pq}{r^3} \hat{i} \]

Step 2: Finding the Net Torque about Point O

The torque on the charge \(-q\) due to the dipole is:

\[ \mathbf{\tau} = -\frac{1}{4\pi\epsilon_0} \frac{pq}{r^2} \hat{k} \]

Answer: The correct option is D.

Answer 2

We are given a situation where a dipole moment \( p = 2aQ \) is formed by two charges, \( +Q \) and \( -Q \), separated by a distance \( 2a \). A third charge \( -q \) is at a distance \( r \) from the dipole, where \( r \gg a \). We are tasked with finding the net force on the charge \( -q \) and the net torque on it about the origin \( O \).
Step 1: Net Force on the Charge \( -q \) The force on a charge \( -q \) due to a dipole is given by the equation: \[ \vec{F} = \frac{1}{4 \pi \epsilon_0} \frac{1}{r^3} \left( 3 \hat{r} (\hat{p} \cdot \hat{r}) - \hat{p} \right) q \] Since \( p = 2aQ \), we substitute \( p \) and calculate the net force acting on the charge. The force on \( -q \) is in the direction of \( \hat{r} \), and the magnitude is proportional to \( \frac{pq}{r^3} \). The direction of this force is along \( \hat{r} \). Thus, the net force on the charge \( -q \) is: \[ \vec{F} = \frac{1}{4 \pi \epsilon_0} \frac{pq \hat{r}}{r^3} \]
Step 2: Net Torque on the Charge \( -q \) The torque \( \vec{\tau} \) on a charge \( q \) placed in the electric field due to a dipole is given by: \[ \vec{\tau} = \vec{r} \times \vec{F} \] The torque is perpendicular to both the position vector \( \vec{r} \) and the force vector \( \vec{F} \). Therefore, the torque on the charge is along \( \hat{k} \), which is perpendicular to the plane formed by \( \hat{r} \) and \( \vec{F} \), and is proportional to \( \frac{pq}{r^2} \). Thus, the net torque on the charge \( -q \) is: \[ \vec{\tau} = \frac{1}{4 \pi \epsilon_0} \frac{pq \hat{k}}{r^2} \]
Conclusion: The net force on the charge \( -q \) is \( \frac{1}{4 \pi \epsilon_0} \frac{pq \hat{r}}{r^3} \), and the net torque is \( \frac{1}{4 \pi \epsilon_0} \frac{pq \hat{k}}{r^2} \).

Thus, the correct answer is option (D).