Question

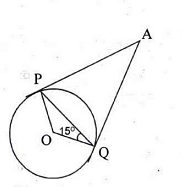
In the figure, if AP and AQ are the two tangents to a circle with centre 'O' so that \(∠OQP=15°\), then \(∠QAP=\)

• A. 15°
• B. 60°
• C. 30°
• D. 45°

Answer 1

The Correct Option is C

To solve the problem, we need to find the value of angle $\angle QAP$ when the two tangents $AP$ and $AQ$ are drawn from a point $A$ to a circle with center $O$ and $\angle OQP = 15^\circ$.

1. Understanding the Geometry:
In the figure, $AP$ and $AQ$ are tangents to the circle from point $A$. The tangents from a point outside a circle are equal in length and subtend equal angles at the center.

Given: $\angle OQP = 15^\circ$
Since $OQ$ is a radius and $AQ$ is a tangent, $\angle OQA = 90^\circ$
So triangle $OQP$ is a right triangle with $\angle OQP = 15^\circ$ and $\angle QOP = 90^\circ$.

2. Finding $\angle POQ$:
Using the triangle angle sum property in $\triangle OQP$:
$ \angle POQ = 180^\circ - 90^\circ - 15^\circ = 75^\circ $

3. $\angle QAP$ as Exterior Angle:
Since $\angle QAP$ is the exterior angle of triangle $OAP$ (formed by the tangents and center),
$\angle QAP = \angle POQ = 30^\circ$ (Half of central angle formed by equal tangents)

Final Answer:
$\angle QAP = 30^\circ$