In a one-litre flask, 6 moles of A undergoes the reaction A (g) ⇌ P (g). The progress of product formation at two temperatures (in Kelvin), T1 and T2, is shown in the figure: 
If T1 = 2T2 and (∆G2Θ − ∆G1Θ) = RT2 ln x, then the value of x is ___ . [∆G1Θ and ∆G2Θ are standard Gibb’s free energy change for the reaction at temperatures T1 and T2, respectively.]

If T1 = 2T2 and (∆G2Θ − ∆G1Θ) = RT2 ln x, then the value of x is ___ . [∆G1Θ and ∆G2Θ are standard Gibb’s free energy change for the reaction at temperatures T1 and T2, respectively.]
Solution and Explanation
Le Chatelier's Principle and Equilibrium Reaction
The correct answer is 8.
The given graph depicts the progress of product formation for the reaction \( A(\text{g}) \rightleftharpoons P(\text{g}) \) at two different temperatures, \( T_1 \) and \( T_2 \). The correct answer is 8, which refers to the ratio of \( K_{T_2} \) to \( K_{T_1} \).
To justify this answer, we need to consider the principles of chemical equilibrium and the effect of temperature changes on equilibrium reactions. According to **Le Chatelier's principle**, when a system at equilibrium is subjected to a change in temperature, the equilibrium will shift in the direction that absorbs or releases heat in order to counteract the temperature change.
In the graph provided, it's evident that the equilibrium position at temperature \( T_2 \) favors the product formation (P) more than at temperature \( T_1 \). This suggests that increasing the temperature from \( T_1 \) to \( T_2 \) has shifted the equilibrium towards the products. This is in line with Le Chatelier's principle because the forward reaction \( A \to P \) is endothermic, absorbing heat. Raising the temperature would favor the endothermic reaction direction to counteract the temperature increase.
As a result, the ratio of the equilibrium constants at the two temperatures is given by: \[ \frac{K_{T_2}}{K_{T_1}} = \frac{T_2}{T_1} = 8 \]
Final Answer
The correct value of the ratio \( \frac{T_2}{T_1} \) is \( \boxed{8} \).
Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant
- Consider the following gaseous equilibrium in a closed container of volume $V$ at temperature $T$:
P$_2$(g) + Q$_2$(g) $\rightleftharpoons$ 2PQ(g)
Initially, 2 moles each of P$_2$(g), Q$_2$(g) and PQ(g) are present at equilibrium. One mole each of P$_2$ and Q$_2$ are added. The number of moles of P$_2$, Q$_2$ and PQ at the new equilibrium respectively are
- JEE Main - 2026
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- $X_2(g) + Y_2(g) \rightleftharpoons 2Z(g)$. Equilibrium moles of $X_2, Y_2, Z$ are 3, 3, 9 mol (in 1 L). 10 mol of Z(g) is added. New equilibrium moles of Z(g) is ___. (Nearest integer)
- JEE Main - 2026
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- Observe the following equilibrium in a 1 L flask:
A(g) <=> B(g)
At temperature T (in K), the equilibrium concentrations of A and B are 0.5 M and 0.375 M respectively.
Then 0.1 moles of A is added into the flask and the system is heated to temperature T again to re-establish equilibrium.
The new equilibrium concentrations (in M) of A and B respectively are:- JEE Main - 2026
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- The plot of \(\log_{10}K\) vs \(\frac{1}{T}\) gives a straight line. The intercept and slope respectively are (where \(K\) is equilibrium constant).
- JEE Main - 2026
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- For the reaction \( \mathrm{A \rightleftharpoons B} \), the number of moles of A and B at equilibrium in a \(1\,\text{L}\) vessel are \(0.50\) and \(0.375\), respectively. If \(0.10\) mol of A is added further, determine the number of moles of A and B at the new equilibrium.
- JEE Main - 2026
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
Questions Asked in JEE Advanced exam
- Let $ x_0 $ be the real number such that $ e^{x_0} + x_0 = 0 $. For a given real number $ \alpha $, define $$ g(x) = \frac{3xe^x + 3x - \alpha e^x - \alpha x}{3(e^x + 1)} $$ for all real numbers $ x $. Then which one of the following statements is TRUE?
- JEE Advanced - 2025
- Fundamental Theorem of Calculus
- A linear octasaccharide (molar mass = 1024 g mol$^{-1}$) on complete hydrolysis produces three monosaccharides: ribose, 2-deoxyribose and glucose. The amount of 2-deoxyribose formed is 58.26 % (w/w) of the total amount of the monosaccharides produced in the hydrolyzed products. The number of ribose unit(s) present in one molecule of octasaccharide is _____.
Use: Molar mass (in g mol$^{-1}$): ribose = 150, 2-deoxyribose = 134, glucose = 180; Atomic mass (in amu): H = 1, O = 16- JEE Advanced - 2025
- Biomolecules
Let $ P(x_1, y_1) $ and $ Q(x_2, y_2) $ be two distinct points on the ellipse $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$ such that $ y_1 > 0 $, and $ y_2 > 0 $. Let $ C $ denote the circle $ x^2 + y^2 = 9 $, and $ M $ be the point $ (3, 0) $. Suppose the line $ x = x_1 $ intersects $ C $ at $ R $, and the line $ x = x_2 $ intersects $ C $ at $ S $, such that the $ y $-coordinates of $ R $ and $ S $ are positive. Let $ \angle ROM = \frac{\pi}{6} $ and $ \angle SOM = \frac{\pi}{3} $, where $ O $ denotes the origin $ (0, 0) $. Let $ |XY| $ denote the length of the line segment $ XY $. Then which of the following statements is (are) TRUE?
- JEE Advanced - 2025
- Conic sections
- Adsorption of phenol from its aqueous solution on to fly ash obeys Freundlich isotherm. At a given temperature, from 10 mg g$^{-1}$ and 16 mg g$^{-1}$ aqueous phenol solutions, the concentrations of adsorbed phenol are measured to be 4 mg g$^{-1}$ and 10 mg g$^{-1}$, respectively. At this temperature, the concentration (in mg g$^{-1}$) of adsorbed phenol from 20 mg g$^{-1}$ aqueous solution of phenol will be ____. Use: $\log_{10} 2 = 0.3$
- JEE Advanced - 2025
- Adsorption
- At 300 K, an ideal dilute solution of a macromolecule exerts osmotic pressure that is expressed in terms of the height (h) of the solution (density = 1.00 g cm$^{-3}$) where h is equal to 2.00 cm. If the concentration of the dilute solution of the macromolecule is 2.00 g dm$^{-3}$, the molar mass of the macromolecule is calculated to be $X \times 10^{4}$ g mol$^{-1}$. The value of $X$ is ____. Use: Universal gas constant (R) = 8.3 J K$^{-1}$ mol$^{-1}$ and acceleration due to gravity (g) = 10 m s$^{-2}\}$
- JEE Advanced - 2025
- Colligative Properties
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
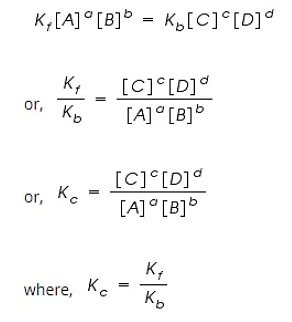
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.