In a class of 60 students, 45 students like music, 50 students like dance and 5 students like neither. Then, the number of students in the class who like both music and dance is
- 35
- 40
- 50
- 55
The Correct Option is B
Solution and Explanation
Let \( M \) represent the number of students who like music, and \( D \) represent the number of students who like dance. From the given data:
Total students = 60
Students who like music \( M = 45 \)
Students who like dance \( D = 50 \)
Students who like neither = 5
Thus, the number of students who like either music or dance or both is: \[ 60 - 5 = 55 \] Now, applying the principle of inclusion and exclusion: \[ M + D - \text{(students who like both music and dance)} = 55 \] Substitute \( M = 45 \) and \( D = 50 \): \[ 45 + 50 - \text{(students who like both music and dance)} = 55 \] Simplifying: \[ 95 - \text{(students who like both music and dance)} = 55 \] \[ \text{(students who like both music and dance)} = 95 - 55 = 40 \]
The correct option is (B): \(40\)
Top Questions on Sets
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
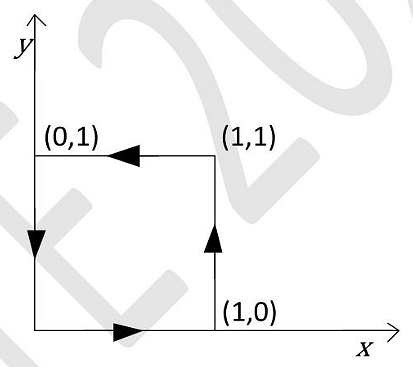
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
Questions Asked in AP POLYCET exam
- The solution of \( x - 2y = 0 \) and \( 3x + 4y - 20 = 0 \) is:
- AP POLYCET - 2025
- Linear Equations
- A prime number \( p \) divides \( a^2 \) where \( a \) is a positive integer, then
- AP POLYCET - 2025
- Prime and Composite Numbers
- Area of a sector of a circle with radius 4 cm and angle 30° is (use \( \pi = 3.14 \)):
- If assumed mean of a data is 47.5, \( \sum f_i d_i = 435 \) and \( \sum f_i = 30 \), then mean of that data is:
- AP POLYCET - 2025
- Arithmetic Mean
- In an electric circuit, three resistors \( 5 \, \Omega \), \( 10 \, \Omega \) and \( 15 \, \Omega \) are connected in series across a \( 60 \, V \) battery. Then the current flowing in the circuit is:
- AP POLYCET - 2025
- Series and Parallel Connection of Resistance