If A=\(\begin{bmatrix}-1&2&3\\5&7&9\\-2&1&1\end{bmatrix}\)and B=\(\begin{bmatrix}-4&1&-5\\1&2&0\\1&3&1\end{bmatrix}\),then verify that
(i)(A+B)'=A'+B'
(ii)(A-B)'=A'-B'
If A=\(\begin{bmatrix}-1&2&3\\5&7&9\\-2&1&1\end{bmatrix}\)and B=\(\begin{bmatrix}-4&1&-5\\1&2&0\\1&3&1\end{bmatrix}\),then verify that
(i)(A+B)'=A'+B'
(ii)(A-B)'=A'-B'
Solution and Explanation
We have: A'=\(\begin{bmatrix}-1&5&-2\\2&7&1\\3&9&1\end{bmatrix}\),B'=\(\begin{bmatrix}-4&1&1\\1&2&3\\-5&0&1\end{bmatrix}\)
(i)A+B= \(\begin{bmatrix}-1&2&3\\5&7&9\\-2&1&1\end{bmatrix}\)+\(\begin{bmatrix}-4&1&-5\\1&2&0\\1&3&1\end{bmatrix}\)
=\(\begin{bmatrix}-5&3&-2\\6&9&9\\1&4&2\end{bmatrix}\)
therefore (A+B)'=\(\begin{bmatrix}-5&6&-1\\3&9&4\\-2&9&2\end{bmatrix}\)
A'+B'=\(\begin{bmatrix}-1&5&-2\\2&7&1\\3&9&1\end{bmatrix}\)+\(\begin{bmatrix}-4&1&1\\1&2&3\\-5&0&1\end{bmatrix}\)
Hence we verified that (A+B)'=A'+B'
(ii)A-B=\(\begin{bmatrix}-1&2&3\\5&7&9\\-2&1&1\end{bmatrix}\)-\(\begin{bmatrix}-4&1&-5\\1&2&0\\1&3&1\end{bmatrix}\)
=\(\begin{bmatrix}3&1&8\\4&5&9\\-3&-2&0\end{bmatrix}\)
therefore (A-B)'=\(\begin{bmatrix}-3&4&-3\\1&5&-2\\8&9&0\end{bmatrix}\)
A'-B'=\(\begin{bmatrix}-1&5&-2\\2&7&1\\3&9&1\end{bmatrix}\)-\(\begin{bmatrix}-4&1&1\\1&2&3\\-5&0&1\end{bmatrix}\)
=\(\begin{bmatrix}-3&4&-3\\1&5&-2\\8&9&0\end{bmatrix}\)
Hence we verified that (A-B)'=A'-B'
Top Questions on Matrices
- The number of $3\times2$ matrices $A$, which can be formed using the elements of the set $\{-2,-1,0,1,2\}$ such that the sum of all the diagonal elements of $A^{T}A$ is $5$, is
- If \[ X=\begin{bmatrix}x\\y\\z\end{bmatrix} \] is a solution of the system of equations $AX=B$, where \[ \text{adj }A= \begin{bmatrix} 4 & 2 & 2\\ -5 & 0 & 5\\ 1 & -2 & 3 \end{bmatrix} \quad \text{and} \quad B=\begin{bmatrix}4\\0\\2\end{bmatrix}, \] then $|x+y+z|$ is equal to
Let \[ f(x)=\int \frac{7x^{10}+9x^8}{(1+x^2+2x^9)^2}\,dx \] and $f(1)=\frac14$. Given that
- For the matrices \( A = \begin{bmatrix} 3 & -4 \\ 1 & -1 \end{bmatrix} \) and \( B = \begin{bmatrix} -29 & 49 \\ -13 & 18 \end{bmatrix} \), if \( (A^{15} + B) \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \), then among the following which one is true?}
- Let the relation \( R \) on the set \( M = \{1, 2, 3, \ldots, 16\} \) be given by \[ R = \{(x, y) : 4y = 5x - 3,\; x, y \in M\}. \] Then the minimum number of elements required to be added in \( R \), in order to make the relation symmetric, is equal to
Questions Asked in CBSE CLASS XII exam
A ladder of fixed length \( h \) is to be placed along the wall such that it is free to move along the height of the wall.
Based upon the above information, answer the following questions:(iii) (b) If the foot of the ladder, whose length is 5 m, is being pulled towards the wall such that the rate of decrease of distance \( y \) is \( 2 \, \text{m/s} \), then at what rate is the height on the wall \( x \) increasing when the foot of the ladder is 3 m away from the wall?
- CBSE CLASS XII - 2025
- Application of derivatives
- A meeting will be held only if all three members A, B and C are present. The probability that member A does not turn up is 0.10, member B does not turn up is 0.20 and member C does not turn up is 0.05. The probability of the meeting being cancelled is:
- CBSE CLASS XII - 2025
- Probability
- Vishesh, Manik and Amit were partners in the ratio 5 : 4 : 1. Amit retired on 31st March, 2024. Vishesh and Manik decided to share Amit’s share in the ratio 2 : 3. What will be the new profit sharing ratio between Vishesh and Manik?
- CBSE CLASS XII - 2025
- Retirement and Death of a Partner
- The electric field in a region is given by \( \vec{E} = 40x \hat{i} \, \text{N/C}. \) Find the amount of work done in taking a unit positive charge from a point (0, 3m) to the point (5m, 0).
- CBSE CLASS XII - 2025
- Electrostatics
- Consider the Linear Programming Problem, where the objective function \[ Z = x + 4y \] needs to be minimized subject to the following constraints: \[ 2x + y \geq 1000, \] \[ x + 2y \geq 800, \] \[ x \geq 0, \quad y \geq 0. \] Draw a neat graph of the feasible region and find the minimum value of $Z$.
- CBSE CLASS XII - 2025
- Linear Programming Problem
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
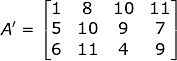
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix