Question

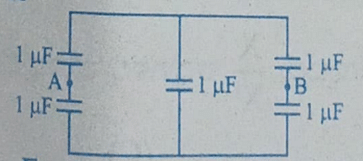
Five capacitors each of value 1 μF are connected as shown in the figure. The equivalent capacitance between A and B is

• A. 1 μF
• B. 2 μF
• C. 5 μF
• D. 3 μF

Answer 1

The Correct Option is A

Given: Five capacitors each of value 1 μF are connected as shown in the figure. The equivalent capacitance between A and B needs to be calculated.

Step-by-Step Solution 

Step 1: Identify the Configuration

We have two sets of capacitors in parallel connected to each other in series.

Step 2: Calculate Equivalent Capacitance of Each Set in Parallel

For the set connected to point A:

\(C_{A} = C_1 + C_2 = 1\,\mu F + 1\,\mu F = 2\,\mu F\)

For the set connected to point B:

\(C_{B} = C_3 + C_4 = 1\,\mu F + 1\,\mu F = 2\,\mu F\)

Step 3: Calculate Equivalent Capacitance of the Series Combination

Since the middle capacitor \( C_5 \) is in series with the parallel combinations, we calculate the equivalent capacitance \( C_{eq} \) as:

\(\frac{1}{C_{eq}} = \frac{1}{C_{A}} + \frac{1}{C_{5}} + \frac{1}{C_{B}}\)

\(\frac{1}{C_{eq}} = \frac{1}{2\,\mu F} + \frac{1}{1\,\mu F} + \frac{1}{2\,\mu F} \\  \frac{1}{C_{eq}} = \frac{1 + 2 + 1}{2\,\mu F} = \frac{4}{2\,\mu F} = \frac{2}{\mu F}\\  C_{eq} = \frac{\mu F}{2} = 0.5\,\mu F\)

Step 4: Final Equivalent Capacitance

The final equivalent capacitance between points A and B is therefore:

\(\boxed{1\,\mu F}\)

Answer 2

1. Identify the Circuit Configuration:
The given circuit is a capacitor network arranged in the form of a Wheatstone bridge. Let the capacitors be denoted as follows:

• \(C_1\): Top-left capacitor (connected to A) = 1 µF
• \(C_2\): Bottom-left capacitor (connected to A) = 1 µF
• \(C_3\): Top-right capacitor (connected to B) = 1 µF
• \(C_4\): Bottom-right capacitor (connected to B) = 1 µF
• \(C_5\): Central capacitor = 1 µF

 

2. Check for Wheatstone Bridge Balance:
For a capacitor Wheatstone bridge, the condition for balance is: \[ \frac{C_1}{C_2} = \frac{C_3}{C_4} \] Substituting the values: \[ \frac{1\,\mu\text{F}}{1\,\mu\text{F}} = \frac{1\,\mu\text{F}}{1\,\mu\text{F}} \] \[ 1 = 1 \] Since the condition is satisfied, the bridge is balanced.

3. Simplify the Balanced Bridge:
In a balanced Wheatstone bridge, the potential difference across the central element (\(C_5\)) is zero. Therefore, no charge accumulates on \(C_5\), and it can be effectively removed from the circuit when calculating the equivalent capacitance between points A and B.

4. Calculate Equivalent Capacitance of the Simplified Circuit:
After removing \(C_5\), the circuit consists of two parallel branches:

• Branch 1: \(C_1\) and \(C_3\) in series.
• Branch 2: \(C_2\) and \(C_4\) in series.

The equivalent capacitance of capacitors in series (\(C_{eq, series}\)) is given by \(\frac{1}{C_{eq, series}} = \frac{1}{C_a} + \frac{1}{C_b} + \dots\).
Equivalent capacitance of Branch 1 (\(C_{13}\)): \[ \frac{1}{C_{13}} = \frac{1}{C_1} + \frac{1}{C_3} = \frac{1}{1\,\mu\text{F}} + \frac{1}{1\,\mu\text{F}} = \frac{2}{1\,\mu\text{F}} \] \[ C_{13} = \frac{1}{2}\,\mu\text{F} = 0.5\,\mu\text{F} \] Equivalent capacitance of Branch 2 (\(C_{24}\)): \[ \frac{1}{C_{24}} = \frac{1}{C_2} + \frac{1}{C_4} = \frac{1}{1\,\mu\text{F}} + \frac{1}{1\,\mu\text{F}} = \frac{2}{1\,\mu\text{F}} \] \[ C_{24} = \frac{1}{2}\,\mu\text{F} = 0.5\,\mu\text{F} \] These two branches (Branch 1 and Branch 2) are connected in parallel between points A and B. The equivalent capacitance of capacitors in parallel (\(C_{eq, parallel}\)) is the sum of individual capacitances: \(C_{eq, parallel} = C_a + C_b + \dots\).
Total equivalent capacitance between A and B (\(C_{AB}\)): \[ C_{AB} = C_{13} + C_{24} = 0.5\,\mu\text{F} + 0.5\,\mu\text{F} = 1\,\mu\text{F} \]

 

Answer: The equivalent capacitance between A and B is 1 µF. This corresponds to option (A).