Question:
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Updated On: Nov 30, 2023
Hide Solution
Verified By Collegedunia
Solution and Explanation
Let the length of the other diagonal of the rhombus be \(x\).
A rhombus is a special case of a parallelogram.
The area of a parallelogram is given by the product of its base and height.
Thus, area of the given rhombus = Base × Height
= 6 cm × 4 cm
= 24 cm2
Also, area of rhombus = \(\frac{1}{2} \) (Product of its diagonals)
24 = \(\frac{1}{2} (x × 8\) cm\()\)
\(x × 4 = 24\)
\(x = 6\) cm
Thus, the length of the other diagonal is 6 cm.
Was this answer helpful?
0
0
Top Questions on Area of a Polygon
- Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
- CBSE Class VIII
- Mathematics
- Area of a Polygon
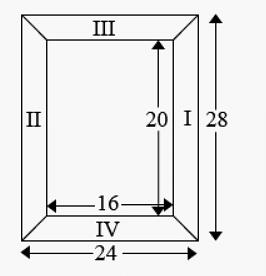
- Diagram of the adjacent picture frame has outer dimensions = 24 cm x 28 cm and inner dimensions 16 cm x 20 cm. Find the area of each section of the frame, if the width of each section is same.
- CBSE Class VIII
- Mathematics
- Area of a Polygon
- Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

- CBSE Class VIII
- Mathematics
- Area of a Polygon
- The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

- CBSE Class VIII
- Mathematics
- Area of a Polygon
- The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
- CBSE Class VIII
- Mathematics
- Area of a Polygon
View More Questions
Questions Asked in CBSE Class VIII exam
- Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
- CBSE Class VIII
- Addition and Subtraction of Algebraic Expressions
- Who had written the letter, to whom, and when?
- CBSE Class VIII
- The Best Christmas Present in the world
- Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
- CBSE Class VIII
- Addition and Subtraction of Algebraic Expressions
- Can the process of rusting be called combustion? Discuss.
- CBSE Class VIII
- Types of Combustion
- Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
- CBSE Class VIII
- Addition and Subtraction of Algebraic Expressions
View More Questions