\(∫\frac{dx}{e^x+e^{-x}}\) is equal to
Show Hint
Let's go through the steps to solve the integral using the substitution method
Given:
\[I = \int \frac{dx}{e^x + e^{-x}}\]
First, rewrite the integrand:
\[I = \int \frac{dx}{e^x + e^{-x}} = \int \frac{dx}{e^x \left(1 + e^{-2x}\right)}\]
Now, make the substitution \( e^x = t \). Therefore, \( dx = \frac{dt}{t} \):
Substitute \( e^x = t \) into the integral:
\[I = \int \frac{dt/t}{t(1 + t^{-2})} = \int \frac{dt}{t^2 + 1}\]
This simplifies to:
\[I = \int \frac{dt}{1 + t^2}\]
The integral of \(\frac{1}{1 + t^2}\) is the arctangent function:
\[I = \arctan(t) + C\]
Now, substitute back \( t = e^x \):
\[I = \arctan(e^x) + C\]
Therefore, the integral \(\int \frac{dx}{e^x + e^{-x}}\) is:
\[I = \arctan(e^x) + C\]
Hence, the correct Answer is Option A\(=tan^{-1}(e^x)+C\)
\(tan^{-1}(e^x)+C\)
\(tan^{-1}(e^{-x})+C\)
\(tan^{-1}(e^x-e^{-x})+C\)
\(log(e^x+e^{-x})+C\)
The Correct Option is A
Solution and Explanation
The correct answer is A:\(=tan^{-1}(e^x)+C\)
Let \(I=∫\frac{dx}{e^x+e^{-x}}dx=∫\frac{e^x}{e^{2x}+1}dx\)
Also,let \(e^x=t⇒e^x dx=dt\)
\(∴I=∫\frac{dt}{1+t^2}\)
\(=tan^{-1}+C\)
\(=tan^{-1}(e^x)+C\)
Hence,the correct Answer is A.
Top Questions on integral
- Find the value of the integral: \[ \int_0^\pi \sin^2(x) \, dx. \]
Let \( f : (0, \infty) \to \mathbb{R} \) be a twice differentiable function. If for some \( a \neq 0 \), } \[ \int_0^a f(x) \, dx = f(a), \quad f(1) = 1, \quad f(16) = \frac{1}{8}, \quad \text{then } 16 - f^{-1}\left( \frac{1}{16} \right) \text{ is equal to:}\]
- Let $ f(x) $ be a positive function and $I_1 = \int_{-\frac{1}{2}}^1 2x \, f\left(2x(1-2x)\right) dx$ and $I_2 = \int_{-1}^2 f\left(x(1-x)\right) dx.$ Then the value of $\frac{I_2}{I_1}$ is equal to ____
- The value of the definite integral \( \int_0^{\pi} \sin^2 x \, dx \) is:
- Evaluate the integral: \[ \int \frac{\sin(2x)}{\sin(x)} \, dx \]
Questions Asked in CBSE CLASS XII exam
“One of these days you’re going to talk yourself into a load of trouble,” her father said aggressively. What do you learn about Sophie’s father from these lines? (Going Places)
- CBSE CLASS XII - 2025
- Literature
- From the following Balance Sheet of Bose Ltd. as at 31st March, 2024, calculate ‘Cash Flows from Operating Activities’.


- CBSE CLASS XII - 2025
- Cash Flow Statement
- Draft an invitation card on behalf of the Principal of J.B. Bhatia Public School for the launch of ‘Yoga for Life’ programme in the school. Mention a compelling highlight of the programme along with other necessary details.
- CBSE CLASS XII - 2025
- Letter Writing
- You are required to design an air-filled solenoid of inductance 0.016 H having a length 0.81 m and radius 0.02 m. The number of turns in the solenoid should be:
- CBSE CLASS XII - 2025
- Electromagnetic induction
- "Under the Ayushmaan Bharat Scheme, the government provides free medical treatment to the poorer section of the society.
"Identify and explain the nature of budget expenditure and its objective in the Ayushmaan Bharat Scheme statement.- CBSE CLASS XII - 2025
- Government Budget and the Economy
Concepts Used:
Definite Integral
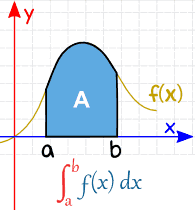
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below: