The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of
coins in each column is also the same.
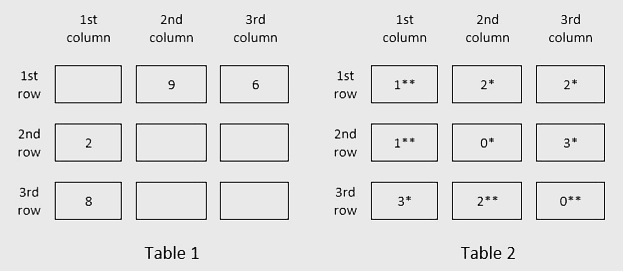
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
How many boxes have at least one sack containing 9 coins?
- 3
- 4
- 5
- 8
The Correct Option is C
Solution and Explanation
- The median for some boxes is given. For any box where the median is 9, there must be at least one sack with 9 coins. These boxes need to be identified from Table 1.
- In Table 2, if a box has the conditions specified with "**" markers, it implies two or more of the conditions are satisfied, including condition (iii), which confirms the presence of a sack with 9 coins.
- Boxes with median 9 from Table 1 automatically qualify.
- Boxes marked with ** in Table 2 should also be included in the count, as they satisfy two or more conditions, including the maximum of 9 coins in at least one sack.
Top Questions on Data Analysis
- Number of socks distributed is approximately what percent of the total number of shoes and the room heaters put together?
- MAT - 2025
- Data Interpretation
- Data Analysis
- Quantity A: 9\% of 93
Quantity B: 93 times 0.09
- MAT - 2025
- Data Interpretation
- Data Analysis
- Quantity A: The sum of integers from -6 to 7
Quantity B: The sum of integers from -7 to 6
- MAT - 2025
- Data Interpretation
- Data Analysis
- Find the wrong number in the series: 2, 10, 30, 68, 130, 232.
- MAT - 2025
- Data Interpretation
- Data Analysis
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station. A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B– C, C– D, and D–E. The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200. The following information is known. 1. Segment C– D had an occupancy factor of 952. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E. 3. Among the seats reserved on segment D– E, exactly four-sevenths were from stations before C. 4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E. 5. No tickets were booked from A to B, from B to D and from D to E. 6. The number of tickets booked for any segment was a multiple of 10.
Questions Asked in CAT exam
- A value of $c$ for which the minimum value of $f(x) = x^2 - 4cx + 8c$ is greater than the maximum value of $g(x) = -x^2 + 3cx - 2c$, is:
- CAT - 2025
- Linear & Quadratic Equations
- In a $\triangle ABC$, points $D$ and $E$ are on the sides $BC$ and $AC$, respectively. $BE$ and $AD$ intersect at point $T$ such that $AD : AT = 4 : 3$, and $BE : BT = 5 : 4$. Point $F$ lies on $AC$ such that $DF$ is parallel to $BE$. Then, $BD : CD$ is:
- CAT - 2025
- Geometry
- In the sequence 1, 3, 5, 7, ..., k, ..., 57, the sum of the numbers up to k, excluding k, is equal to the sum of the numbers from k up to 57, also excluding k. What is k?
- CAT - 2025
- Arithmetic Progression
- Find the number of integer pairs (x, y) that satisfy the following system of inequalities:
\[ \begin{cases} x \geq y \geq 3 \\ x + y \leq 14 \end{cases} \]
- CAT - 2025
- Linear & Quadratic Equations
- The monthly sales of a product from January to April were 120, 135, 150 and 165 units, respectively. The cost price of the product was Rs. 240 per unit, and a fixed marked price was used for the product in all the four months. Discounts of 20%, 10% and 5% were given on the marked price per unit in January, February and March, respectively, while no discounts were given in April. If the total profit from January to April was Rs. 138825, then the marked price per unit, in rupees, was
- CAT - 2025
- Profit and Loss